Codeforces Round #249 (Div. 2) (ABCD题解)

时间：2015-07-17 02:03:00 阅读：607 评论：0 收藏：0 [点我收藏+]

It‘s that time of the year when the Russians flood their countryside summer cottages (dachas) and the bus stop has a lot of people. People rarely go to the dacha on their own, it‘s usually a group, so the people stand in queue by groups.

The bus stop queue has n groups of people. The i-th group from the beginning has a_i people. Every 30 minutes an empty bus arrives at the bus stop, it can carry at most m people. Naturally, the people from the first group enter the bus first. Then go the people from the second group and so on. Note that the order of groups in the queue never changes. Moreover, if some group cannot fit all of its members into the current bus, it waits for the next bus together with other groups standing after it in the queue.

Your task is to determine how many buses is needed to transport all n groups to the dacha countryside.

Input

The first line contains two integers n and m (1?≤?n,?m?≤?100). The next line contains n integers: a₁,?a₂,?...,?a_n (1?≤?a_i?≤?m).

Output

Print a single integer — the number of buses that is needed to transport all n groups to the dacha countryside.

Sample test(s)

Input

4 3
2 3 2 1

Output

Input

3 4
1 2 1

Output

题目大意：一共n个站台，每个站台一开始有ai个人，一辆车一次最多载m个人，如果当前这辆车不能装下当前站的所有人，则当前站的人都不上车而等下一辆，问搭载所有的人需要几辆车

题目分析：照着题意模拟即可

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

int a[105];

int main()
{
    int n, m;
    scanf("%d %d", &n, &m);
    for(int i = 0; i < n; i++)
        scanf("%d", &a[i]);
    int ans = 1;
    int now = m;
    for(int i = 0; i < n;)
    {
        if(a[i] <= now)
        {
            now -= a[i];
            i ++;
        }
        else
        {
            now = m;
            ans ++;
        }
    }
    printf("%d\n", ans);
}

Pasha has a positive integer a without leading zeroes. Today he decided that the number is too small and he should make it larger. Unfortunately, the only operation Pasha can do is to swap two adjacent decimal digits of the integer.

Help Pasha count the maximum number he can get if he has the time to make at most k swaps.

Input

The single line contains two integers a and k (1?≤?a?≤?10¹⁸; 0?≤?k?≤?100).

Output

Print the maximum number that Pasha can get if he makes at most k swaps.

Sample test(s)

Input

1990 1

Output

Input

300 0

Output

Input

1034 2

Output

Input

9090000078001234 6

Output

9907000008001234

题目大意：给一个数a，每次只能交换相邻两个数，最多交换k次，求交换后的最大数字

题目分析：贪心问题，显然大数字往前放的贪心策略是错的，正确的应该是尽量让高位的数字大，从最高位开始向低位找，先找到k步之内的最大数，如果k步之内的最大数不是当前位置的数，那么把最大数交换到当前为止，没交换一次，k减1

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

char s[20];
int k;

int main()
{
    scanf("%s %d", s, &k);
    int len = strlen(s);
    int now;
    for(int i = 0; i < len; i++)
    {
        now = i;
        for(int j = i + 1; j <= i + k && j < len; j++)
            if(s[j] > s[now])
                now = j;
        if(now != i)
        {
            for(int j = now; j > i; j--)
            {
                swap(s[j], s[j - 1]);
                k --;
            }
        }
    }
    printf("%s\n", s);
}

In this problem, your task is to use ASCII graphics to paint a cardiogram.

A cardiogram is a polyline with the following corners:

$技术分享$

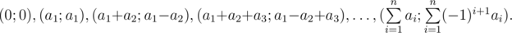
That is, a cardiogram is fully defined by a sequence of positive integers a₁,?a₂,?...,?a_n.

Your task is to paint a cardiogram by given sequence a_i.

Input

The first line contains integer n (2?≤?n?≤?1000). The next line contains the sequence of integers a₁,?a₂,?...,?a_n (1?≤?a_i?≤?1000). It is guaranteed that the sum of all a_i doesn‘t exceed 1000.

Output

Print max |y_i?-?y_j| lines (where y_k is the y coordinate of the k-th point of the polyline), in each line print 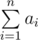$技术分享$ characters. Each character must equal either ??/?? (slash), ? \ ? (backslash), ? ? (space). The printed image must be the image of the given polyline. Please study the test samples for better understanding of how to print a cardiogram.

Note that in this problem the checker checks your answer taking spaces into consideration. Do not print any extra characters. Remember that the wrong answer to the first pretest doesn‘t give you a penalty.

Sample test(s)

Input

5
3 1 2 5 1

Output

     ?/?\     
  ?/?\?/?  \    
 ?/?      \   
?/?        \  
          \?/?

Input

3
1 5 1

Output

?/?\     
  \    
   \   
    \  
     \?/?

Note

Due to the technical reasons the answers for the samples cannot be copied from the statement. We‘ve attached two text documents with the answers below.

http://assets.codeforces.com/rounds/435/1.txt

http://assets.codeforces.com/rounds/435/2.txt

题目大意：这题意着实醒神。。。给一个数列，按其顺序一上一下打印图形

题目分析：因为还好ai最大是1000，可以用一个2000*2000的矩阵存起来，然后就模拟吧，注意动态取竖直方向的最大最小值，没想到cf还有这样的题

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
char g[2005][2005];

int main()
{
    int n;
    scanf("%d", &n);
    int sign = 1;
    int maxy = 1000, miny = 1000;
    int x = -1, y = 1000;
    memset(g, 0, sizeof(g));
    while(n--)
    {
        int a;
        scanf("%d", &a);
        if(sign == 1)
            y --;
        else
            y ++;
        for(int i = 1; i <= a; i++)
        {
            if(sign == 1)
            {
                y ++;
                x ++;
                g[x][y] = '/';
            }
            else
            {
                y --;
                x ++;
                g[x][y] = '\\';
            }
        }
        maxy = max(maxy, y);
        miny = min(miny, y);
        sign *= -1;
    }
    for(int i = 0; i <= x; i++)
        for(int j = miny; j <= maxy; j++)
            if(!g[i][j])
                g[i][j] = ' ';
            int cnt =0 ;
    for(int j = maxy; j >= miny; j--)
    {
        for(int i = 0; i <= x; i++)
            printf("%c", g[i][j]);
        printf("\n");
    }
}

You are given an n?×?m grid, some of its nodes are black, the others are white. Moreover, it‘s not an ordinary grid — each unit square of the grid has painted diagonals.

The figure below is an example of such grid of size 3?×?5. Four nodes of this grid are black, the other 11 nodes are white.

$技术分享$

Your task is to count the number of such triangles on the given grid that:

the corners match the white nodes, and the area is positive;
all sides go along the grid lines (horizontal, vertical or diagonal);
no side contains black nodes.

Input

The first line contains two integers n and m (2?≤?n,?m?≤?400). Each of the following n lines contain m characters (zeros and ones) — the description of the grid. If the j-th character in the i-th line equals zero, then the node on the i-th horizontal line and on the j-th vertical line is painted white. Otherwise, the node is painted black.

The horizontal lines are numbered starting from one from top to bottom, the vertical lines are numbered starting from one from left to right.

Output

Print a single integer — the number of required triangles.

Sample test(s)

Input

Output

Input

2 2
00
00

Output

Input

2 2
11
11

Output

Note

The figure below shows red and blue triangles. They are the examples of the required triangles in the first sample. One of the invalid triangles is painted green. It is invalid because not all sides go along the grid lines.

$技术分享$

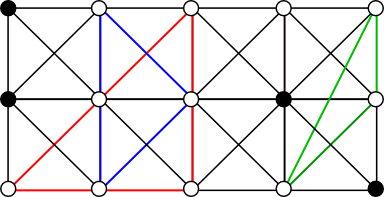
题目大意：给个0/1矩阵，0的地方可以相互连接，问矩阵中共有多少个三角形，注意三角形的边必须是垂直水平或者斜45度的

题目分析：做的特别纠结的一题，根据题意显然所有三角形都是直角三角形，所以可以直接枚举直角来做，我说下我的做法吧。。。

我是枚举边做的，首先预处理出每个点往其周围的8个方向可以延伸的最远距离（距离及点数），用dp[i][j][0-7]表示，然后分成两种情况，第一种是只有一个边是斜45度方向的，枚举全部情况，注意这种情况我是按45度角枚举的，所以最后要除2，然后是有两条斜45度方向边的情况，这种情况是按90度枚举的，所以不会重复，其实直接全部枚举直角就可以了，我做的时候调来调去给调乱了，就搞成了这样

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int const MAX = 405;
int dp[MAX][MAX][8], g[MAX][MAX];
char s[MAX][MAX];

int main()
{
    int n, m;
    scanf("%d %d", &n, &m);
    memset(dp, 0, sizeof(dp));
    for(int i = 1; i <= n; i++)
    {   
        scanf("%s", s[i] + 1);
        for(int j = 1; j <= m; j++)
        {
            g[i][j] = s[i][j] - '0';
            if(!g[i][j])
                for(int k = 0; k < 8; k++)
                    dp[i][j][k] = 1;
        }
    }
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            if(dp[i - 1][j][0] && dp[i][j][0])
                dp[i][j][0] += dp[i - 1][j][0];
            if(dp[i - 1][j - 1][7] && dp[i][j][7])
                dp[i][j][7] += dp[i - 1][j - 1][7];
            if(dp[i][j - 1][6] && dp[i][j][6])
                dp[i][j][6] += dp[i][j - 1][6];
        }
        for(int j = m; j >= 1; j--)
        {
            if(dp[i - 1][j + 1][1] && dp[i][j][1])
                dp[i][j][1] += dp[i - 1][j + 1][1];
            if(dp[i][j + 1][2] && dp[i][j][2])
                dp[i][j][2] += dp[i][j + 1][2];
        }
    }
    for(int i = n; i >= 1; i--)
    {
        for(int j = 1; j <= m; j++)
        {
            if(dp[i + 1][j][4] && dp[i][j][4])
                dp[i][j][4] += dp[i + 1][j][4];
            if(dp[i + 1][j - 1][5] && dp[i][j][5])
                dp[i][j][5] += dp[i + 1][j - 1][5];
        }
        for(int j = m; j >= 1; j--)
        {
            if(dp[i + 1][j + 1][3] && dp[i][j][3])
                dp[i][j][3] += dp[i + 1][j + 1][3];
        }
    }
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            for(int k = 0; k < 8; k++)
                dp[i][j][k] -= 1;
    int ans1 = 0;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            for(int k = 1; k <= max(n, m); k++)
            {
                if(dp[i][j][0] >= k && dp[i][j][7] >= k && i - k >= 1 && dp[i - k][j][6] >= k)
                    ans1 ++;
                if(dp[i][j][0] >= k && dp[i][j][1] >= k && i - k >= 1 && dp[i - k][j][2] >= k)
                    ans1 ++;
                if(dp[i][j][2] >= k && dp[i][j][1] >= k && j + k <= m && dp[i][j + k][0] >= k)
                    ans1 ++;
                if(dp[i][j][2] >= k && dp[i][j][3] >= k && j + k <= m && dp[i][j + k][4] >= k)
                    ans1 ++;
                if(dp[i][j][4] >= k && dp[i][j][3] >= k && i + k <= n && dp[i + k][j][2] >= k)
                    ans1 ++;
                if(dp[i][j][4] >= k && dp[i][j][5] >= k && i + k <= n && dp[i + k][j][6] >= k)
                    ans1 ++;
                if(dp[i][j][6] >= k && dp[i][j][5] >= k && j - k >= 1 && dp[i][j - k][4] >= k)
                    ans1 ++;
                if(dp[i][j][6] >= k && dp[i][j][7] >= k && j - k >= 1 && dp[i][j - k][0] >= k)
                    ans1 ++;
            }
        }
    }
    ans1 /= 2;
    int ans2 = 0;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            for(int k = 1; k <= max(n, m); k++)
            {

                if(dp[i][j][1] >= k && dp[i][j][3] >= k && i - k >= 1 && j + k <= m && dp[i - k][j + k][4] >= 2 * k)
                    ans2 ++;
                if(dp[i][j][5] >= k && dp[i][j][3] >= k && i + k <= n && j - k >= 1 && dp[i + k][j - k][2] >= 2 * k)
                    ans2 ++;
                if(dp[i][j][5] >= k && dp[i][j][7] >= k && i - k >= 1 && j - k >= 1 && dp[i - k][j - k][4] >= 2 * k)
                    ans2 ++;
                if(dp[i][j][1] >= k && dp[i][j][7] >= k && i - k >= 1 && j - k >= 1 && dp[i - k][j - k][2] >= 2 * k)
                    ans2 ++;
            }
        }
    }
    printf("%d\n", ans1 + ans2);
}

Codeforces Round #249 (Div. 2) (ABCD题解)

标签：codeforces

原文地址：http://blog.csdn.net/tc_to_top/article/details/46919643

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行