标签:style blog http color width os
如果一条线段的端点是有次序之分的话,那么这种线段就称为 有向线段,如果有向线段p1p2的起点p1在坐标的原点,则可以把它称为矢量 p2
设二维矢量 P = (x1, y1), Q = (x2, y2),则 P + Q = (x1 + x2, y1 + y2), P - Q = (x1 - x2, y1 - y2),且有 P + Q = Q + P, P - Q = -(Q - P)
设矢量 P = (x1, y1), Q = (x2, y2),则 P * Q = x1 * y2 - x2 * y1; 其结果是一个由 (0, 0), P, Q, P + Q 所组成的平行四边形的 带符号的面积,P * Q = -(Q * P), P * (- Q) = -(P * Q)
叉积的一个非常重要的性质是可以通过它的符号来判断两矢量相互之间的顺逆时针关系:
若 P * Q > 0,则 P 在 Q 的顺时针方向
若 P * Q < 0, 则 P 在 Q 的逆时针方向
若 P * Q = 0,则 P 与 Q 共线,但不确定 P, Q 的方向是否相同
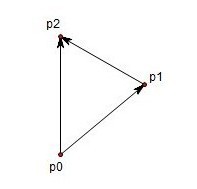
如图,假设有折线段 p0p1p2 ,要确定 p1p2 相对于 p0p1 是向左拐还是向右拐,可以通过计算(p2 - p0)*(p1 - p0) 的符号来确定折线的拐向(点 p2 - p0 实际上就是向量 p2,但这里要注意线段和矢量的区别)
设点 Q = (x, y), P1 = (x1, y1), P2 = (x2, y2),若 (Q - P1)*(P2 - P1) = 0 且 min(x1, x2) <= x <= max(x1, x2) && min(y1, y2) <= y <= max(y1, y2),则点 Q 在线段 P1P2 上
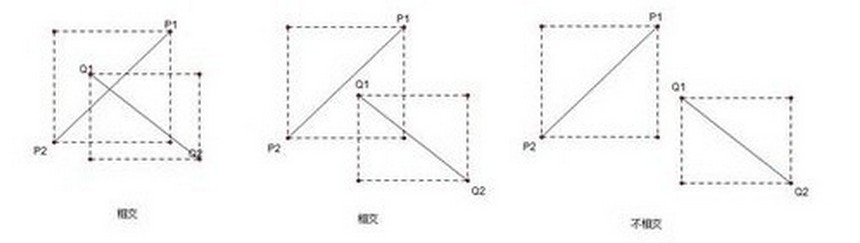
设以线段 P1P2 为对角线的矩形为 R,设以线段 Q1Q2 为对角线的矩形为 T,若 R、T 不相交,则两线段不可能相交
假设 P1 = (x1, y1), P2 = (x2, y2), Q1 = (x3, y3), Q2 = (x4, y4),设矩形 R 的 x 坐标的最小边界为 minRX = min(x1, x2),以此类推,将矩形表示为 R = (minRX, minRY, maxRX, maxRY) 的形式,若两矩形相交,则相交的部分构成了一个新的矩形 F,如图所示,我们可以知道 F 的 minFX = max(minRX, minTX), minFY = max(minRY, minTY), maxFX = min(maxRX, maxTX), maxFY = min(maxRY, maxTX),得到 F 的各个值之后,只要判断矩形 F 是否成立就知道 R 和 T 到底有没有相交了,若 minFX > maxFX 或 minFY > maxFy 则 F 无法构成,RT不相交,否则 RT相交
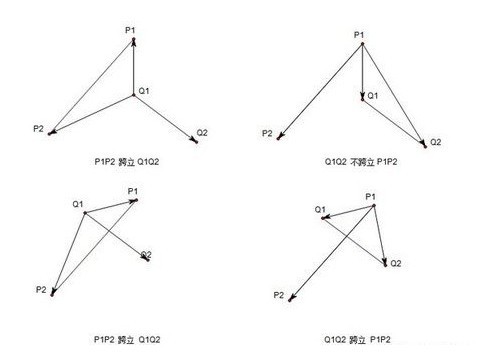
若 P1P2 跨立 Q1Q2,则 P1,P2 分别在 Q1Q2 所在直线的两端,则有 (P1 - Q1)*(Q2 - Q1) * (Q2 - Q1)*(P2 - Q1) > 0,当 (P1 - Q1)*(Q2 - Q1) = 0 时,说明 (P1 - Q1) 与 (Q2 - Q1) 共线,但由于已经经过快速排斥试验,所以 Q1 必为 P1P2 与 Q1Q2 的交点,依然满足线段相交的条件,则跨立试验可改为:
当 (P1 - Q1)*(Q2 - Q1) * (Q2 - Q1)*(P2 - Q1) >= 0,则 P1P2 跨立 Q1Q2,当 Q1Q2 也跨立 P1P2 的时候,则 P1P2 相交
(注意式子中被隔开的 * 代表两个叉积的值的相乘,而另外的两个 * 则代表计算矢量叉积)
首先引出计算几何学中一个最基本的问题:如何判断向量在
的顺时针方向还是逆时针方向?
把p0定为原点,p1的坐标是(x1,y1),p2的坐标是(x2,y2)。向量的叉积(cross product)实际上就是矩阵的行列式:
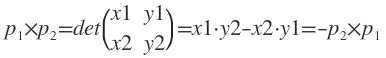
当叉积为正时,说明在
的顺时针方向上;叉积为0说明两向量共线(同向或反向)。
当同时满足:
(1)和
在
的两侧(即一个顺时针方向上,一个在逆时针方向上)
(2)和
在
的两侧
时可肯定和
相交。
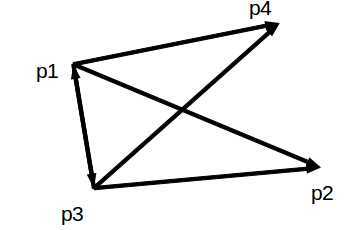
图1
图1是线段相交的一般情形。
图2只满足第(1)条,不满足第(2)条所以不能证明和
相交。
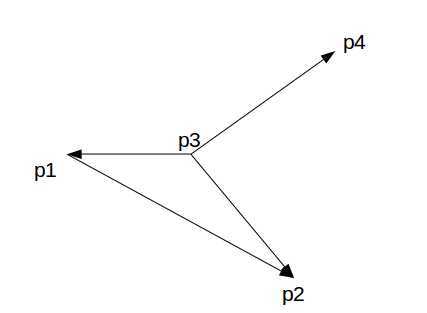
图2
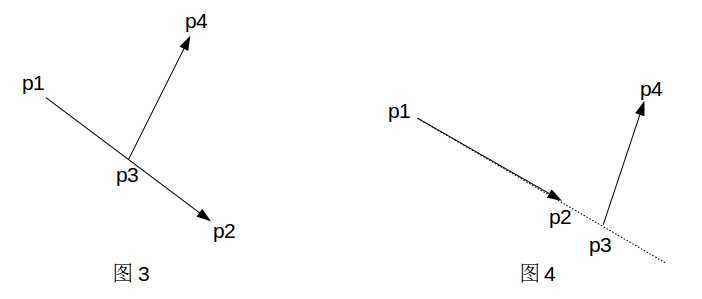
图3和图4是一种特殊情况,它不满足第(2)条,因为和
重合,即
和
的叉积为0。
#include "stdafx.h" typedef struct point { int x; int y; }vector; struct line{ point start; point end; }; struct rec{ int up; int down; int left; int right; }; int max(int x, int y) { return x>y ? x : y; } int min(int x, int y) { return x<y ? x : y; } vector VectorSubtraction(vector a, vector b){ vector v; v.x = a.x - b.x; v.y = a.y - b.y; return v; } line VectorToLine(vector a){ line l; l.start.x = 0; l.start.y = 0; l.end.x = a.x; l.end.y = a.y; return l; } vector LineToVector(line a){ vector v; v.x = a.end.x - a.start.x; v.y = a.end.y - a.start.y; return v; } rec LineToRec(line a){ //将一条线段构造成一个有四条边界的矩形 rec ra; ra.left = min(a.start.x, a.end.x); ra.right = max(a.start.x, a.end.x); ra.down = min(a.start.y, a.end.y); ra.up = max(a.start.y, a.end.y); return ra; } rec VectorToRec(vector v){ return LineToRec(VectorToLine(v)); } int IsCrossRec(rec a, rec b){ //快速排斥实验 rec c;//假设相交了 c.left = max(a.left, b.left); c.right = min(a.right, b.right); c.down = max(a.down, b.down); c.up = min(a.up, b.up); if (c.left <= c.right&&c.down <= c.up){//如果相交矩形存在或者为一个点,则两矩形a,b相交,否则不相交,一条线的情况显然线段不会相交 return 1; } else return 0; } int CrossProduct(vector a, vector b){ return a.x*b.y - a.y*b.x; } int IsBetween(vector a, vector b, vector c){ //跨立实验,判定向量a是否在b、c之间,考虑共线的问题 if (CrossProduct(a, b)*CrossProduct(a,c)<0) { return 1; } else if (CrossProduct(a, b) == 0 && (IsCrossRec(VectorToRec(a), VectorToRec(c)) || IsCrossRec(VectorToRec(b), VectorToRec(c)))){ return 1;//借用相交矩形函数解决是否在线段上的问题 } else if (CrossProduct(a, c) == 0 && (IsCrossRec(VectorToRec(a), VectorToRec(b)) || IsCrossRec(VectorToRec(c), VectorToRec(b)))){ return 1; } else { return 0; } } int SegmentIntersect(line a, line b){ point p1, p2, p3, p4; if (!IsCrossRec(LineToRec(a), LineToRec(b)))return 0; p1 = a.start; p2 = a.end; p3 = b.start; p4 = b.end; if (IsBetween(VectorSubtraction(p4, p3), VectorSubtraction(p2, p3), VectorSubtraction(p1, p3)) && IsBetween(VectorSubtraction(p2, p1), VectorSubtraction(p3, p1), VectorSubtraction(p4, p1))){ //向量的减法得出新的向量然后判定方位 return 1; } return 0; } int _tmain(int argc, _TCHAR* argv[]) { line a, b; printf("输入线段a的x点的横纵坐标如\"0 0\"\n"); scanf("%d %d",&a.start.x,&a.start.y); printf("输入线段a的y点的横纵坐标如\"0 0\"\n"); scanf("%d %d",&a.end.x,&a.end.y); printf("输入线段b的x点的横纵坐标如\"0 0\"\n"); scanf("%d %d",&b.start.x,&b.start.y); printf("输入线段b的y点的横纵坐标如\"0 0\"\n"); scanf("%d %d",&b.end.x,&b.end.y); if (SegmentIntersect(a, b)){ printf("Y\n"); } else { printf("N\n"); } return 0; }
标签:style blog http color width os
原文地址:http://www.cnblogs.com/holyshawn/p/3830221.html