标签：
题意是要求出一个串的第k大的半回文子串
半回文串的定义是：若一个串其实位置为1，那么当所有奇数位i，且i<=(s.length+1/2)，满足s[i]=s[s.length-i+1]的时候，
那么这个串就是半回文串。
作法就是，把这个串的所有半回文子串建成一个字典树，然后查第k大就好了
#include<map>
#include<string>
#include<cstring>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<queue>
#include<vector>
#include<iostream>
#include<algorithm>
#include<bitset>
#include<climits>
#include<list>
#include<iomanip>
#include<stack>
#include<set>
using namespace std;
struct node
{
char val;
int vis,sum;
node *next[2];
};
string s,ans;
void dfs(node *now,int k)
{
if(now->val<'c')
{
ans+=now->val;
k-=now->vis;
if(k<1)
return;
}
if(now->next[0]==NULL)
{
if(now->next[1]==NULL)
return;
dfs(now->next[1],k);
}
else
{
if(now->next[1]==NULL)
dfs(now->next[0],k);
else
{
if(now->next[0]->sum>=k)
dfs(now->next[0],k);
else
dfs(now->next[1],k-now->next[0]->sum);
}
}
}
bool dp[5010][5010];
void Dp(int n)
{
for(int i=0;i<n;i++)
dp[i][i]=1;
for(int i=1;i<n;i++)
if(s[i-1]==s[i])
dp[i-1][i]=1;
for(int i=2;i<n;i++)
if(s[i-2]==s[i])
dp[i-2][i]=1;
for(int i=3;i<n;i++)
if(s[i-3]==s[i])
dp[i-3][i]=1;
for(int i=5;i<=n;i++)
for(int j=0;j+i-1<n;j++)
if(s[j]==s[j+i-1]&&dp[j+2][j+i-3])
dp[j][j+i-1]=1;
}
int bg,ed;
void add(node *now,int index)
{
for(int i=0;i<2;i++)
if(s[index]=='a'+i)
{
if(now->next[i]==NULL)
{
now->next[i]=new node;
memset(now->next[i],0,sizeof(node));
now->next[i]->val=s[index];
}
if(index==ed)
{
now->next[i]->vis++;
now->next[i]->sum++;
}
else
{
if(dp[bg][index])
{
now->next[i]->vis++;
now->next[i]->sum++;
}
add(now->next[i],index+1);
}
}
now->sum=now->vis;
for(int i=0;i<2;i++)
if(now->next[i]!=NULL)
now->sum+=now->next[i]->sum;
}
int main()
{
cin>>s;
int k;
cin>>k;
int n=s.length();
Dp(n);
node *fs=new node;
memset(fs,0,sizeof(node));
fs->val='c';
for(int i=0;i<n;i++)
for(int j=n-1;j>=i;j--)
if(dp[i][j])
{
bg=i;
ed=j;
add(fs,i);
break;
}
dfs(fs,k);
cout<<ans;
}Tomorrow Ann takes the hardest exam of programming where she should get an excellent mark.
On the last theoretical class the teacher introduced the notion of a half-palindrome.
String t is a half-palindrome, if for all the odd positions i (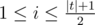
)
the following condition is held: ti?=?t|t|?-?i?+?1,
where |t| is the length of string t if
positions are indexed from 1. For example, strings "abaa",
"a", "bb", "abbbaa"
are half-palindromes and strings "ab", "bba"
and "aaabaa" are not.
Ann knows that on the exam she will get string s, consisting only of letters a and b, and number k. To get an excellent mark she has to find the k-th in the lexicographical order string among all substrings of s that are half-palyndromes. Note that each substring in this order is considered as many times as many times it occurs in s.
The teachers guarantees that the given number k doesn‘t exceed the number of substrings of the given string that are half-palindromes.
Can you cope with this problem?
The first line of the input contains string s (1?≤?|s|?≤?5000), consisting only of characters ‘a‘ and ‘b‘, where |s| is the length of string s.
The second line contains a positive integer k — the lexicographical number of the requested string among all the half-palindrome substrings of the given string s. The strings are numbered starting from one.
It is guaranteed that number k doesn‘t exceed the number of substrings of the given string that are half-palindromes.
Print a substring of the given string that is the k-th in the lexicographical order of all substrings of the given string that are half-palindromes.
abbabaab 7
abaa
aaaaa 10
aaa
bbaabb 13
bbaabb
By definition, string a?=?a1a2... an is lexicographically less than string b?=?b1b2... bm, if either a is a prefix of b and doesn‘t coincide withb, or there exists such i, that a1?=?b1,?a2?=?b2,?... ai?-?1?=?bi?-?1,?ai?<?bi.
In the first sample half-palindrome substrings are the following strings — a, a, a, a, aa, aba, abaa, abba, abbabaa, b, b, b, b, baab,bab, bb, bbab, bbabaab (the list is given in the lexicographical order).
版权声明：本文为博主原创文章，未经博主允许不得转载。
codeforces 557 E Ann and Half-Palindrome
标签：
原文地址：http://blog.csdn.net/stl112514/article/details/46952295
