如何产生1-100 之间的100个不重复的随机数

标签：

1：首先从原始数组中随机选择一个数字，然后将该数字从数组中剔除，再随记选，再剔除，重复99次，就解决了。

    我们知道从数组中剔除一个元素的复杂度为O（N)，那么随机选取n个数字，它的复杂度就是O(N²)了。

2：用hash作为中间过滤层，因为在数组中，我们采用随机数的话，也许随机数在多次随机中可能会有重复，所以需要用hash来判断一下，

    如果在hash中重复，则继续产生随机数，直到不重复为止，当然这个复杂度就不好说了，得要看随机数随机不随机了，好的话,O(N)搞定，

    不走运的话无上限~

3：就像标题说的一样，很多问题我们都能在现实生活中找到写照，毕竟很多东西是来源于现实，又抽象于现实，比如这个题目在现实生活中，

　 可以对应到的就是“洗扑克牌”，在算法中也叫“洗牌原理”，我们知道洗扑克牌的方式就是随机的交换扑克牌的位置，又叫做"切牌",当你切了

   很多次后，我们的扑克牌就可以认为是足够乱了，复杂度也就变成了O(N)，用代码实现就是这样的。

   <1> 先有序的生成52张牌，然后有序的放到数组中。

   <2>从1-52中随机的产生一个数，然后将当前次数的位置跟随机数的位置进行交换，重复52次，我们的牌就可以认为足够乱了。

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;

namespace ConsoleApplication1
{
    public class Program
    {
        static void Main(string[] args)
        {
            CardClass cc = new CardClass();

            cc.NewCard();

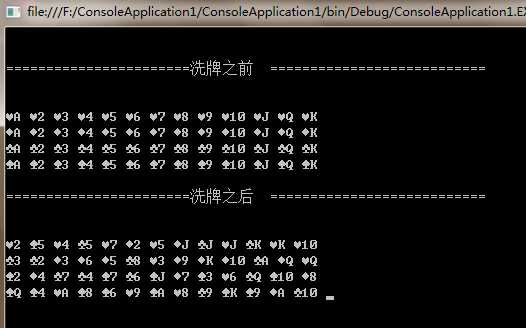
            Console.WriteLine("\n\n=======================洗牌之前  ===========================\n");
            cc.Output();

            Console.WriteLine("\n\n=======================洗牌之后  ===========================\n");
            cc.Shuffle();
            cc.Output();


            Console.Read();
        }
    }

    public class CardClass
    {
        public Card[] card = new Card[52];

        /// <summary>
        /// 具体扑克牌
        /// </summary>
        public class Card
        {
            public char suit;

            public string num;
        }

        /// <summary>
        /// 开牌
        /// </summary>
        public void NewCard()
        {
            for (int i = 1; i <= card.Length; i++)
            {
                var suit = ((i - 1) / 13) + 3;
                var num = i % 13;

                string temp;

                switch (num)
                {
                    case 1: temp = "A"; break;
                    case 11: temp = "J"; break;
                    case 12: temp = "Q"; break;
                    case 0: temp = "K"; break;
                    default: temp = num.ToString(); break;
                }

                card[i - 1] = new Card()
                {
                    suit = (char)suit,
                    num = temp
                };
            }
        }

        /// <summary>
        /// 洗牌
        /// </summary>
        public void Shuffle()
        {
            for (int i = 0; i < card.Length; i++)
            {
                var rand = new Random((int)DateTime.Now.Ticks).Next(0, card.Length);

                //因为随机数是伪随记，正真的随机数是要跟硬件打交道的，所以这里设置了停留1ms
                System.Threading.Thread.Sleep(1);

                var temp = card[rand];

                card[rand] = card[i];

                card[i] = temp;
            }
        }

        /// <summary>
        /// 输入牌型
        /// </summary>
        public void Output()
        {
            for (int i = 0; i < card.Length; i++)
            {
                if (i % 13 == 0)
                    Console.WriteLine();

                Console.Write("{0}{1} ", card[i].suit, card[i].num);
            }
        }
    }
}

如何产生1-100 之间的100个不重复的随机数

标签：

原文地址：http://blog.csdn.net/djd1234567/article/details/46944955