标签:
矩阵快速幂
首先我是用暴力DFS算了一下前20项、找到规律F(n)=F(n-1)+F(n-3)+F(n-4)。
接下来运用矩阵快速幂。
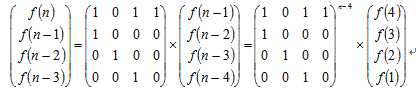
#include<cstdio> #include<cstring> #include<cmath> #include<algorithm> using namespace std; int n; int m; int R,C; struct Matrix { int A[10][10]; Matrix operator*(Matrix b); }; Matrix Matrix::operator*(Matrix b) { Matrix c; memset(c.A,0,sizeof(c.A)); int i,j,k; for(i=1; i<=R; i++) for(j=1; j<=C; j++) for(k=1; k<=4; k++) c.A[i][j]=((A[i][k]*b.A[k][j])%m+c.A[i][j])%m; return c; } int main() { int i,j; while(~scanf("%d%d",&n,&m)) { if(0<=n&&n<=4) { if(n==0) printf("0\n"); if(n==1) printf("%d\n",2%m); if(n==2) printf("%d\n",4%m); if(n==3) printf("%d\n",6%m); if(n==4) printf("%d\n",9%m); } else { Matrix c; for(i=1; i<=4; i++) for(j=1; j<=4; j++) { if(i==j) c.A[i][j]=1; else c.A[i][j]=0; } Matrix a; a.A[1][1]=1;a.A[1][2]=0;a.A[1][3]=1;a.A[1][4]=1; a.A[2][1]=1;a.A[2][2]=0;a.A[2][3]=0;a.A[2][4]=0; a.A[3][1]=0;a.A[3][2]=1;a.A[3][3]=0;a.A[3][4]=0; a.A[4][1]=0;a.A[4][2]=0;a.A[4][3]=1;a.A[4][4]=0; R=4;C=4; int b=n-4; while(b!=0) { if(b%2==1) c=c*a,b--; else a=a*a,b=b/2; } Matrix B; B.A[1][1]=9;B.A[2][1]=6; B.A[3][1]=4;B.A[4][1]=2; R=4; C=1; Matrix ans; ans=c*B; printf("%d\n",ans.A[1][1]); } } return 0; }
标签:
原文地址:http://www.cnblogs.com/zufezzt/p/4658348.html