质因数分解

标签：style   blog   class   code   java   ext   

如何分析问题、解决问题？

一个质因数分解的小问题。

如果给定一个数，如果是质数，则除了1和它本身，就没有其他乘积因子了；如果是合数，则一定能变成若干个质数相乘的形式。因此质因数分解就是把一个数分解成很多个质数因子的过程。

刚碰到这个问题的时候的想法是：给一个数，然后用质数去除它。但是问题又来了，怎么知道一个数是否为质数呢？或者说如何自动生成一个质数来作除数呢？总不可能先给一个自己写一个数组然后自己敲一些质数进去，每次要除的时候再一个一个检查过去吧？而且不可能把所有的质数都敲进去。这显然不是一个好方法。

前段时间做ACM，有道题有部分是关于判断一个数是否为质数的。

public static boolean isPrime(int num) {
        int temp;
        for (int i = 2; i < num; i++) {
            temp = num % i;
            if (temp == 0)
                return false;
        }

        return true;
    }

由此联想，先判断一个数是否为素数，然后再拿这个数来作除数怎么样？这样至少解决了自动生成质数的问题。

但是，如果一个数可以分解成很多个因子，如420可以分解成 2 2 3 5 7 ，如果每次分解都要先一大堆运算来生成质数，然后再来做除法，显然是一个复杂度很大的算法。因此这又不是一个好方法。

其实我们的思路有时候被问题本身的表达形式给限制住了，因此很多时候无法做到思维发散。

就像这个问题，质因数分解，要用一个个质数去除，首先要有质数。一定要这样吗？

质数的定义是什么？则除了1和它本身，就没有其他乘积因子了。

那我们可以从另一个角度来找解决方案：

package temp;

import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        Scanner inNum = new Scanner(System.in);
        int num = inNum.nextInt();
        int y = 2;
        while (num != 1) {
            if (num % y == 0) {
                num = num / y;
                System.out.print(y + "\t");
            } else {
                y++;
            }
        }
    }
}

从中可以看到，并不需要特意去找一个质数，而是从2开始除就好了，设被除数（任意给定的数）为num，当num被除得没有2的因子之后，再将除数+1，即y++，继续做除法。不用担心结果中会出现4、6、15、24……这些情况，因为，这些本身就是合数，举例来说，假设num能被6 = 2*3 整除，说明num可以被2或3整除，而做num = num/y的前提是y=6，即y>2且y>3，也即num已经被除得没有2和3的因子了。

因此这个算法是从小到大一步步找出所有质因数，而不是先列出质数然后一个个去除。从某中角度上来说像是跳过了中间多余的环节。

跳过中间多余环节，就像《浪潮之巅》中所写的，戴尔/阿里巴巴都做到了省去了一大部分中间流通环节，因此使成本大大降低，并直接或间接地从中获益。

（现在一想，其实一开始学因数分解的时候也是用的这种方法，如果是偶数先用2开始除，然后……

 ）

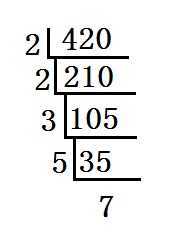写到这儿，主要不是说找到了一个很好的解决分解质因数的方法，

而是从不同的角度切入问题，试着找到更好的解决方案。

质因数分解,布布扣,bubuko.com

质因数分解

标签：style   blog   class   code   java   ext   

原文地址：http://www.cnblogs.com/Cmfvacks-IsLjj/p/3705242.html