标签:
为了彻底理解树状数组,试着用树状数组做了下普通平衡树
而树状数组只能离线做,或者保证值的大小在数组可承受的范围内也是可以的,因为要求离线是因为必须事前对所有数离散化。
然后我们看刘汝佳蓝书上的图
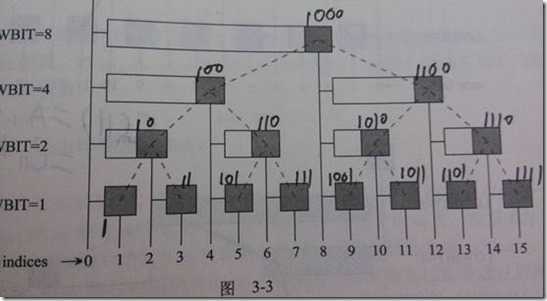
利用如下代码,可以找到所有前缀和中第一个大于等于k的
1 int kth(int k) { 2 int ans=0; 3 for(int i=20;i>=0; --i) { 4 ans += 1<<i; 5 if(ans>=sz || C[ans]>=k) ans-=1<<i; 6 else k-=C[ans]; 7 } 8 return seq[ans+1]; 9 }
什么原理呢,我们这么理解,把树状数组看成一棵树,事实上他的节点编号的中序遍历是有序的,跟平衡树有异曲同工之妙,假设现在在(1000)2这个点,如果往左走,就相当于没有取[1,8],接着在[1,7]中取,如果往右走,就相当于取了[1,8],接着在[9,15]中取,至于应该往左走还是往右走跟平衡树找第k大是一样的。然后可以发现,平衡树相当于是在[1,n]上建树的,而二叉索引树是在[1,2^k](k为2^k>=n的最小正整数)。
给出普通平衡树的完整代码
1 #include<iostream> 2 #include<cstring> 3 #include<cstdlib> 4 #include<cstdio> 5 #include<algorithm> 6 7 using namespace std; 8 9 const int Maxn=100010; 10 11 int C[Maxn],sz; 12 13 int sum(int x) { 14 int ret=0; 15 for(;0<x && x<=sz; x-=x&-x) ret+=C[x]; 16 return ret; 17 } 18 19 void add(int x,int d) { 20 for(;0<x&&x<=sz; x+= x&-x) C[x]+=d; 21 } 22 23 int seq[Maxn],tot; 24 void HashInit() { 25 sort(seq+1,seq+tot+1); 26 sz = unique (seq+1,seq+tot+1) - (seq+1); 27 } 28 int hash(int x) { 29 return lower_bound(seq+1,seq+sz+1,x) - seq; 30 } 31 32 int opt[Maxn],num[Maxn]; 33 34 int kth(int k) { 35 int ans=0; 36 for(int i=20;i>=0; --i) { 37 ans += 1<<i; 38 if(ans>=sz || C[ans]>=k) ans-=1<<i; 39 else k-=C[ans]; 40 } 41 return seq[ans+1]; 42 } 43 44 int main() { 45 #ifdef DEBUG 46 freopen("in.txt","r",stdin); 47 // freopen("out.txt","w",stdout); 48 #endif 49 50 int n; 51 scanf("%d",&n); 52 for(int i=1;i<=n;i++) { 53 scanf("%d%d",opt+i,num+i); 54 if(opt[i]!=4) seq[++tot] = num[i]; 55 } 56 57 HashInit(); 58 59 for(int i=1;i<=n;i++) { 60 if(opt[i]==1) add(hash(num[i]),1); 61 if(opt[i]==2) add(hash(num[i]),-1); 62 if(opt[i]==3) printf("%d\n",sum(hash(num[i])-1)+1); 63 if(opt[i]==4) printf("%d\n",kth(num[i])); 64 if(opt[i]==5) printf("%d\n",kth(sum(hash(num[i])-1))); 65 if(opt[i]==6) printf("%d\n",kth(sum(hash(num[i]))+1)); 66 } 67 68 return 0; 69 }
标签:
原文地址:http://www.cnblogs.com/showson/p/4665775.html