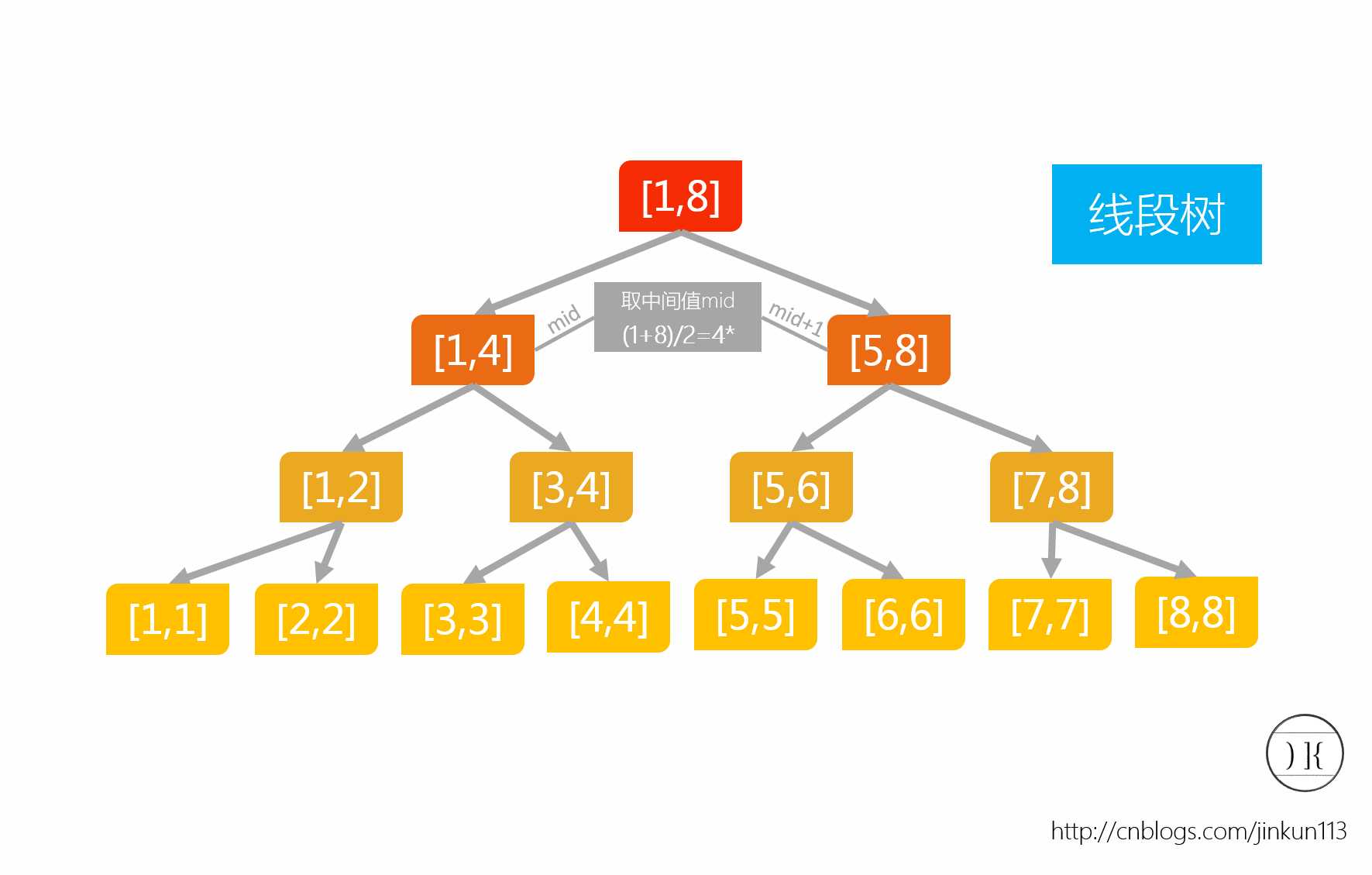
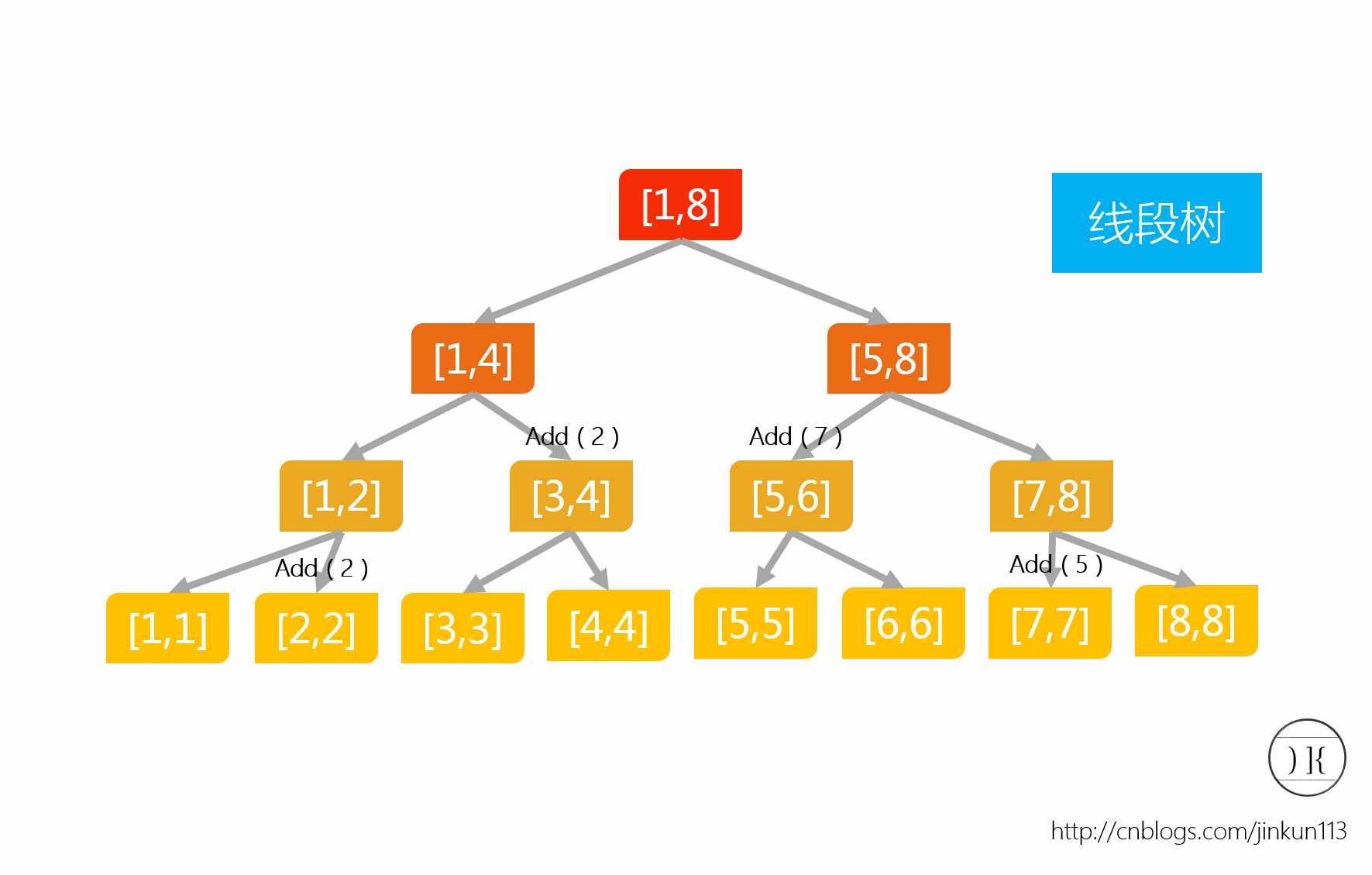
void update2(int now,int l,int r,int ql,int qr,int val) // 区间修改,ql和qr为查询部分,val为增加的值
{
if (l==ql && r==qr) { tree[now].sum+=val*(r-l+1),tree[now].lazy+=val; return; } // 如果当前的线段就是所求
int mid=(l+r)/2;
if (tree[now].lazy!=0) pushDown(now,r-l+1); // 下放
if (l<=ql && mid>=qr) update2(now*2,l,mid,ql,qr,val); // 如果所求线段包含于当前线段的左儿子
else if (mid+1<=ql && r>=qr) update2(now*2+1,mid+1,r,ql,qr,val); // 右儿子
else // 所求线段在左儿子右儿子均有一部分,所以可以分开更新
{
update2(now*2,l,mid,ql,mid,val);
update2(now*2+1,mid+1,r,mid+1,qr,val);
}
tree[now].sum=tree[now*2].sum+tree[now*2+1].sum; // 上放
}
-------------------------------------------------------------------------------------------------------
区间加减相对而言就有点麻烦了。先不管pushDown函数。麻烦之处是在于线段树本身的一个优化,如果没有这个优化,线段树的效率就会变低。我们考虑到一个问题:假设一开始在[2,6]内增加2,又在[5,7]内增加5,那么在[5,6]内不要相当于增加7?在暂时没有询问操作的情况下,我们可以偷一点懒——对于每一条线段,加一个lazy标识,当没有询问的时候,可以不需要去对树进行更新。
在更新的时候,我们不进行线段树本身值的加减,只修改变量lazy。也许我的思路相对于复杂一些,但是一样可以正常理解啦。。
没看懂?其实可以说得很形象:秋天到了,你是庙里的一个和尚,方丈给你一个任务:扫院子里的落叶。众所周知,落叶在秋天是会不断落下的,所以扫了一遍之后,过不一阵子就又有叶子了。在方丈还没有来检查你的工作的情况下,你可以偷一点懒——让叶子堆积在那里!反正早扫晚扫都是扫,还不如晚扫呢是不?(还没懂你还是弃疗算了。。)
现在,pushDown函数的作用可否知道了?那就是将当前线段保存的lazy标识释放出来,对线段树进行真正值的更新。什么时候要用到?如果你明白了其原理应该已经知道了——两种情况,当你需要对标了lazy标识的线段树的子节点进行操作,你不得不进行更新了;当需要进行查询操作时(就是当方丈过来的时候= =),进行更新。
-----------------------------------------------------------------------------------------------------------------
void pushDown(long long now,long long m) // 区间修改——lazy标记下放
{
tree[now*2].lazy+=tree[now].lazy; tree[now*2+1].lazy+=tree[now].lazy;
tree[now*2].sum+=tree[now].lazy*(m-(m/2));
tree[now*2+1].sum+=tree[now].lazy*(m/2);
tree[now].lazy=0;
}
-----------------------------------------------------------------------------------------------------------------
<3>单点查询
直接上代码。
-----------------------------------------------------------------------------------------------------------------
int getVal(int now,int l,int r,int loc) // 单点查询
{
int mid=(l+r)/2;
if (l==r && r==loc) return tree[now].val;
else if (loc>=l && loc<=mid) return getVal(now*2,l,mid,loc);
else return getVal(now*2+1,mid+1,r,loc);
}
-----------------------------------------------------------------------------------------------------------------
<4>查询区间和/最大值/最小值
也没什么难的,就是需要注意到前面提到的pushDown函数需要在这里用到。
-----------------------------------------------------------------------------------------------------------------
int getSum(int now,int l,int r,int ql,int qr) // 区间和
{
if (l==ql && r==qr) return tree[now].sum;
int mid=(l+r)/2,ans;
if (tree[now].lazy!=0) pushDown(now,r-l+1);
if (ql>=l && qr<=mid) ans=getSum(now*2,l,mid,ql,qr);
else if (ql>=mid+1 && qr<=r) ans=getSum(now*2+1,mid+1,r,ql,qr);
else ans=getSum(now*2,l,mid,ql,mid)+getSum(now*2+1,mid+1,r,mid+1,qr);
return ans;
}
-----------------------------------------------------------------------------------------------------------------
这里只给出了区间和的代码,最大值最小值同理,大家自己去写了。
线段树就这么讲完了,完整的代码就是通过上述函数组合起来就可以了。