标签:
基本概念
二叉搜索树是以一棵二叉树来组织的。这样的一棵树可以使用一个链表数据结构来表示:
其中每个节点就是一个对象,除了key和data之外,每个节点还包含left、right和p属性,分别指向节点的左孩子、右孩子和双亲。
二叉搜索树的性质:对于任何结点x,其左子树中的关键字最大不超过x.key,其右子树的关键字最小不低于x.key。
二叉搜索树性质允许我们通过一个简单的递归算法来按序输出二叉搜索树中的所有关键字,这种算法称为中序遍历算法。
INORDER-TREE-WALK(x) if x≠NIL INORDER-TREE-WALK(x.left) print x.key INORDER-TREE-WALK(x.right)
调用INORDER-TREE-WALK(T.root)就可以输出一个二叉搜索树中的所有元素。
查询二叉搜索树
查找:我们使用下面过程在一棵二叉搜索树中查找一个具有给定关键字的结点。
输入一个指向树根的指针和一个关键字k,如果这个结点存在,TREE-SERACH返回一个指向关键字为k的结点的指针;否则返回NIL。
TREE-SEARCH(x.k) if x==NIL or k==x.key return x if k<x.key return TREE-SERACH(x.left,k) else return TREE-SERACH(x.right,l)
这个过程从树根开始查找。对于遇到的每个结点x,比较关键字k与x.key:
如果两个关键字相等,查找就终止。
如果k小于x.key,查找在x的左子树继续。因为二叉搜索树的性质,所以k不能被存储在右子树中。
如果k大于x.key,查找在x的右子树继续。
我们可以采用while循环来展开递归,用一种迭代方式重写这个过程。对于大多数计算机,迭代版本的效率要高很多
ITERATIVE-TREE-SEARCH(x,k) while x≠NIL and k≠x.key if x<x.key x=x.left else x=x.right return x
最大关键字元素和最小关键字元素
通过从树根开始沿着left孩子指针知道遇到一个NIL,二叉搜索树的性质保证了下面代码可以找到最小关键字元素
TREE-MINIMUM(x) while x.left≠NIL x=x.left return x
寻找最大关键字元素的伪代码是对称的
TREE-MAXIMUM(x) while x.right≠NIL x=x.right return x
后继和前驱
给定一棵二叉搜索树中的一个结点,有时候需要按中序遍历的次序查找它的后继。后继是指该结点的下一个结点。
TREE-SUCCESSOR(x) if x.right≠NIL return TREE-MINIMUM(x.right) y=x.p while y≠NIL and x==y.right x=y y=y.p return y
TREE-SUCCESSOR分为两种情况:
1.如果结点x的右子树非空,那么x的后继恰是x右子树中的最左结点(调用TREE-MINIMUM(x.right)可以找到)
2.如果结点x的右子树为空并有一个后继y,那么y就是x的有左孩子的最底层祖先(x的后继y是x的最底层祖先,并且其左孩子也是x的祖先)。
在下图中,关键字为13的结点的后继是关键字为15的结点。为了找到y,只需简单地从x开始沿树而上直到遇到一个有左孩子的结点(并且其左孩子也是x的祖先)。
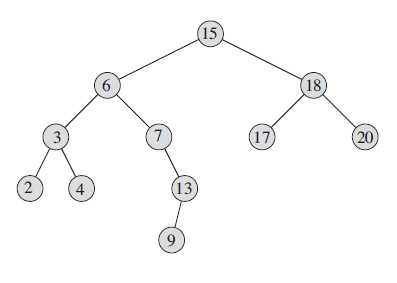
插入
要将一个新值v插入到一棵二叉搜索树T中,需要调用TREE-INSERT。
该过程以结点z作为输入,其中z.key=v,z.left=NIL,z.right=NIL。这个过程要修改T和z的某些属性,来把z插入到树中的相应位置
TREE-INSERT(T,z) y=NIL x=T.root while x≠NIL y=x if z.key<x.key x=x.left else x=x.right z.p=y if y==NIL T.root=z //tree T was empty else if z.key<y.key y.left=z else y.right=z
TREE-INSERT从树根开始,根据z.key和x.key的比较结果决定向左或向右移动
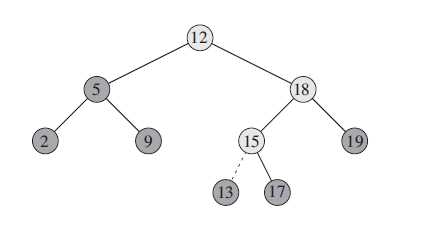
删除
从一棵二叉搜索树T中删除一个结点z分为3种基本情况:
1.如果z没有孩子结点,那么只是简单地将它删除,并修改它的父结点,用NIL作为孩子来替换z
2.如果z只有一个孩子,那么僵这个孩子提升到树中z的位置上,并修改z的父结点,用z的孩子来替换z
3.如果z有两个孩子,那么找z的后继y(一定在z的右子树中),并让y占据树中z的位置。z的原来右子树部分称为y的新的右子树,并且z的左子树称为y的新的左子树。
第三种基本情况分为两种:
我们查找z的后继y,这个后继位于z的右子树中并且没有左孩子。
1.如果y是z的右孩子,那么用y替换z,原来z的左孩子称为y的左孩子
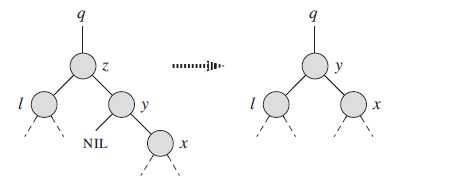
2.如果y并不是z的右孩子。则先用y的右孩子替换y,然后用y替换z
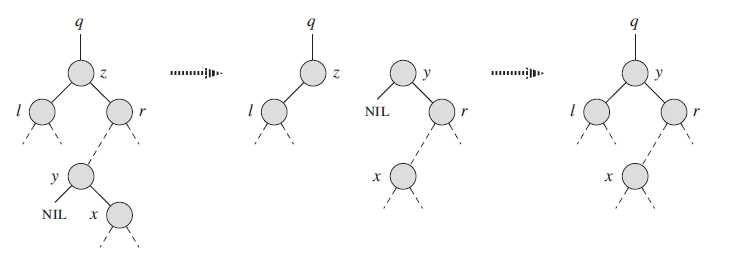
为了在二叉搜索树内移动子树,定义一个子过程TRANSPLANT,它是用另一棵子树替换一棵子树并成为其双亲的孩子结点。
当TRANSPLANT用一棵以v为根的子树来替换一棵以u为根的子树时,结点u的双亲就变为结点v的双亲,并且最后v成为u的双亲的相应孩子
TRANSPLANT(T,u,v) if u.p==NIL //u是T的树根的情况 T.root=v else if u==u.p.left //如果u是其双亲的左孩子,则设置u双亲的左孩子为v u.p.left=v else u.p.right=v //如果u是其双亲的右孩子,则设置u双亲的右孩子为v if v≠NIL //设置v的双亲为u的双亲 v.p=u.p
利用现成的TRANSPLANT过程,下面是从二叉搜索树T中删除结点z的删除过程
TREE-DELETE(T,z) //只有一个孩子的情况 if z.left==NIL TRANSPLANT(T,z,z.right) else if z.right==NIL TRANSPLANT(T,z,z.left) //有两个孩子的情况 else y=TREE-MINIMUM(z.right) //如果y并不是z的右孩子,则先执行if里面的代码 if y.p≠z TRANSPLANT(T,y,y.right) y.right=z.right y.right.p=y TRANSPLANT(T,z,y) y.left=z.left y.left.p=y
实现与测试代码
定义数据结构和建树函数

1 typedef struct node 2 { 3 int key; 4 int data; 5 node *left; 6 node *right; 7 node *parent; 8 }*BSTree; 9 10 BSTree tree_build(int k,int d) 11 { 12 //初始化根结点 13 node *t=new node(); 14 t->key=k; 15 t->data=d; 16 t->left=NULL; 17 t->right=NULL; 18 t->parent=NULL; 19 return t; 20 }
插入函数

1 void tree_insert(BSTree t,int k,int d) 2 { 3 //初始化插入结点 4 node *z=new node(); 5 z->key=k; 6 z->data=d; 7 z->left=NULL; 8 z->right=NULL; 9 z->parent=NULL; 10 //x是当前结点,y用来记录插入位置的父结点 11 node *y=NULL; 12 node *x=t; 13 //找到插入结点的父结点,并用y记录起来 14 while(x!=NULL) 15 { 16 y=x; 17 if(z->key<x->key) 18 x=x->left; 19 else 20 x=x->right; 21 } 22 //插入结点 23 z->parent=y; 24 if(z->key<y->key) 25 y->left=z; 26 else 27 y->right=z; 28 }
中序遍历函数

1 void tree_inorder(BSTree t) 2 { 3 if(t!=NULL) 4 { 5 tree_inorder(t->left); 6 cout<<"key:"<<t->key<<" data:"<<t->data<<endl; 7 tree_inorder(t->right); 8 } 9 }
查找函数

1 node *tree_search(BSTree t,int key) 2 { 3 while(t!=NULL&&key!=t->key) 4 { 5 if(key<t->key) 6 t=t->left; 7 else 8 t=t->right; 9 } 10 return t; 11 }
最大/小关键字元素和后继

1 node *tree_minimum(BSTree t) 2 { 3 while(t->left!=NULL) 4 t=t->left; 5 return t; 6 } 7 8 node *tree_maximum(BSTree t) 9 { 10 while(t->right!=NULL) 11 t=t->right; 12 return t; 13 } 14 15 node *tree_next(node *x) 16 { 17 if(x->right!=NULL) 18 return tree_minimum(x->right); 19 node *y=x->parent; 20 while(y!=NULL&&x==y->right) 21 { 22 x=y; 23 y=y->parent; 24 } 25 return y; 26 }
删除函数

1 void tree_transplant(BSTree *t,node *u,node *v) 2 { 3 if(u->parent==NULL) 4 *t=v; 5 else if(u==u->parent->left) 6 u->parent->left=v; 7 else 8 u->parent->right=v; 9 if(v!=NULL) 10 v->parent=u->parent; 11 } 12 13 void tree_delete(BSTree *t,node *z) 14 { 15 if(z->left==NULL) 16 tree_transplant(t,z,z->right); 17 else if(z->right==NULL) 18 tree_transplant(t,z,z->left); 19 else 20 { 21 node *y=NULL; 22 y=tree_minimum(z->right); 23 if(y->parent!=z) 24 { 25 tree_transplant(t,y,y->right); 26 y->right=z->right; 27 y->right->parent=y; 28 } 29 tree_transplant(t,z,y); 30 y->left=z->left; 31 y->left->parent=y; 32 } 33 delete z; 34 }
测试代码

1 int main() 2 { 3 BSTree t=tree_build(3,20); 4 cout<<"inorder:"<<endl; 5 tree_insert(t,1,50); 6 tree_insert(t,4,30); 7 tree_insert(t,2,10); 8 tree_insert(t,5,40); 9 tree_inorder(t); 10 cout<<endl; 11 int key=3; 12 cout<<"search:\nkey="<<key<<" data="<<tree_search(t,key)->data<<endl<<endl; 13 cout<<"minimum:data="<<tree_minimum(t)->data<<endl; 14 cout<<"maximum:data="<<tree_maximum(t)->data<<endl; 15 node *next=tree_next(tree_search(t,key)); 16 cout<<"next:key="<<key<<" the next key="<<next->key<<" data="<<next->data<<endl<<endl; 17 tree_delete(&t,tree_search(t,key)); 18 cout<<"after delete:"<<endl; 19 tree_inorder(t); 20 return 0; 21 }
标签:
原文地址:http://www.cnblogs.com/runnyu/p/4677902.html