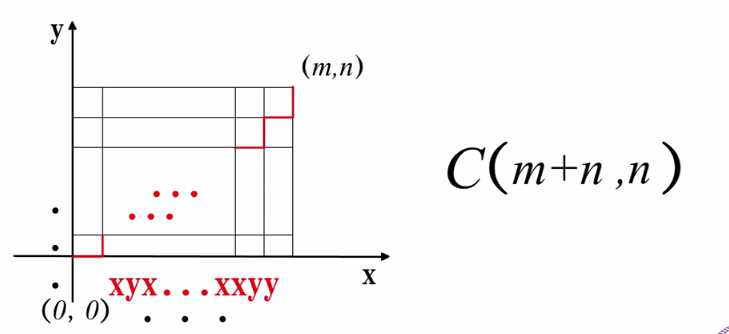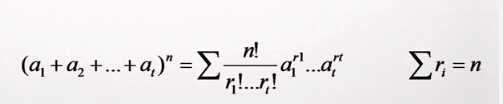标签:
如下图所示的格路模型,从(0,0)到(m,n)的不同途径可以看成是在由x,y(分别代表x,y方向的一段路)组成的长度为m+n的字符串中选择m个作为x的位置,那么不同的路径数就是C(m+n,n).
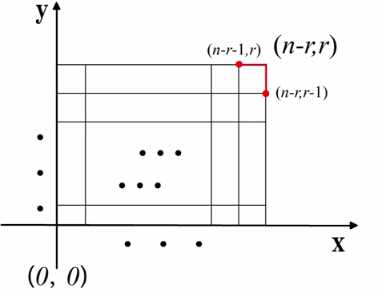
组合关系式C(n,r) = C(n-1,r)+C(n-1,r-1)也可以由格路模型得出,如下图所示,从(0,0)到(n-r,r)的路径数等于从(0,0)--->(n-r-1,r),(0,0)--->(n-r,r-1)之和。
圆排列:从n个数中取r个的圆排列数为P(n,r)/r,2<=r<=n;项链排列,P(n,r)/2r.
多重全排列,若干个元素,r1个1,r2个2,...,rt个t的全排列数P(n;r1,r2...rt)=n!/r1!r2!...rt!,可用于计算多项式展开的系数,如下图所示。
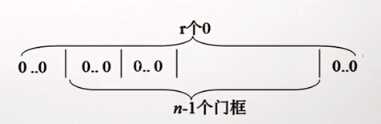
从n个元素中取r个的可重组合,用隔板法模型可以得出,组合数等于C(n+r-1,r).
对于可重组合和不相邻组合(从1,2,...,n取r个不相邻元素)可以构造出对应的无重组合,如下图所示,c序列的取值范围为[1,n-r+1],且无重复,那么从从原序列取不相邻的b1-br的组合数相当于从c序列中取r个元素,即C(n-r+1,r).
以下是各种排列和组合的计算方法,可重与多重的区别是,可重的可取元素是无限的,多重拿来排列的元素是确定的,有限的。
关于全排列以及相关的算法在另一篇博客中说明。
排列与组合
标签:
原文地址:http://www.cnblogs.com/louwqtc/p/permutation-combination.html