标签:
1.定义:
在有向图G中,如果两个顶点间至少存在一条路径,称两个顶点强连通(SC---strongly connected)。
有向图中的极大强连通子图,成为强连通分量(SCC---strongly connected components)。
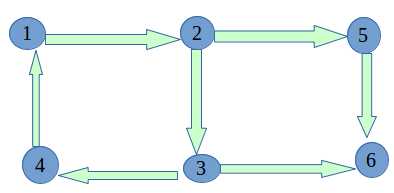
下图中,子图{1,2,3,4}为一个强连通分量,因为顶点1,2,3,4两两可达,{5},{6}也分别是两个强连通分量。
2.tarjan算法
tarjan算法的基础是DFS。我们准备两个数组Low和Dfn。Low数组是一个标记数组,记录该点所在的强连通子图所在搜索子树的根节点的 Dfn值,Dfn数组记录搜索到该点的时间,也就是第几个搜索这个点的。根据以下几条规则,经过搜索遍历该图(无需回溯)和 对栈的操作,我们就可以得到该有向图的强连通分量。

///其时间复杂度也是O(N+M) #include <stdio.h> #include <string.h> #include <vector> #include <stack> #include <iostream> using namespace std; #define N 10005 /// 题目中可能的最大点数 stack<int>sta; /// 存储已遍历的结点 vector<int>gra[N]; /// 邻接表表示图 int dfn[N]; /// 深度优先搜索访问次序 int low[N]; /// 能追溯到的最早的次序 int InStack[N]; /// 检查是否在栈中(2:在栈中,1:已访问,且不在栈中,0:不在) vector<int> Component[N]; /// 获得强连通分量结果 int InComponent[N]; /// 记录每个点在第几号强连通分量里 int Index,ComponentNumber;/// 索引号,强连通分量个数 int n, m; /// 点数,边数 void init()///清空容器,数组 { memset(dfn, 0, sizeof(dfn)); memset(low, 0, sizeof(low)); memset(InStack, 0, sizeof(InStack)); Index = ComponentNumber = 0; for (int i = 1; i <= n; ++ i) { gra[i].clear(); Component[i].clear(); } while(!sta.empty()) sta.pop(); } void tarjan(int u) { InStack[u] = 2; low[u] = dfn[u] = ++ Index; sta.push(u);///寻找u所在的强连通分量 for (int i = 0; i < gra[u].size(); ++ i) { int t = gra[u][i]; if (dfn[t] == 0)///不在的继续递归 { tarjan(t);///递归到头了就 low[u] = min(low[u], low[t]); } else if (InStack[t] == 2)///在栈里 { low[u] = min(low[u], dfn[t]); } } if(low[u] == dfn[u])///sta出栈就是一个强连通分量的 { ++ComponentNumber;///强连通分量个数 while (!sta.empty()) { int j = sta.top(); sta.pop(); InStack[j] = 1;///已访问但不在栈中 Component[ComponentNumber].push_back(j); ///用vector存储第ComponentNumber个强连通分量 InComponent[j]=ComponentNumber; ///记录每个点在第几号强连通分量里 if (j == u) break; } } } void input(void) { for(int i=1; i<=m; i++) { int a,b; scanf("%d%d",&a,&b); gra[a].push_back(b);///有向图才有强连通分量 } } void solve(void) { for(int i=1; i<=n; i++) if(!dfn[i]) tarjan(i); if(ComponentNumber > 1) puts("No"); else puts("Yes"); } int main() { while(scanf("%d%d",&n,&m),n+m) { init(); input(); solve(); /*每一个强连通分量的具体数字 for(int i = 1; i <= ComponentNumber; i++) { for(int j = 0; j < Component[i].size(); j++) if(!j) cout << Component[i][j]; else cout <<"-->"<< Component[i][j]; cout<<endl; } */ } return 0; }
本文来源http://blog.csdn.net/xinghongduo/article/details/6195337
标签:
原文地址:http://www.cnblogs.com/ACMERY/p/4679807.html