标签:
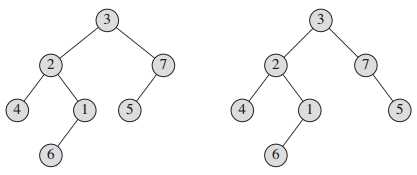
We define binary trees recursively. A binary tree T is a structure defined on a finite set of nodes that either contains no nodes, or is composed of three disjoint sets of nodes: a root node, a binary tree called its left subtree, and a binary tree called its right subtree.
我们递归地来定义二叉树。二叉树T是定义在有限结点集上的结构,它或者不包含任何结点,或者包含三个不相交的结点集合:一个根结点,一棵称为左子树的二叉树,以及一棵称为右子树的二叉树。
In computer science, a binary tree is a tree data structure in which each node has at most two children, which are referred to as the left child and the right child. A recursive definition using just set theory notions is that a (non-empty) binary tree is a triple (L, S, R), where L and R are binary trees or the empty set and S is a singleton set.Some authors allow the binary tree to be the empty set as well.
在计算机科学中,二叉树是一种树形的数据结构,它每个结点最多拥有两个子树,这两个子树被称为左子树和右子树。一种用集合的理论观点的递归定义是,二叉树是一个三元集合(L,S,R),并且L和R均为二叉树集合或空集,S为单元素集。一些作者允许二叉树为一个空集。
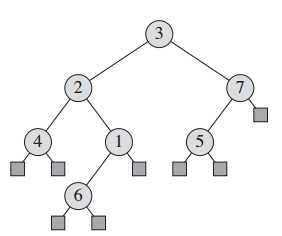
The tree that results is a full binary tree: each node is either a leaf or has degree exactly 2.
Full Binary Tree:每个结点是叶节点或者度为2。
A full binary tree (sometimes proper binary tree or 2-tree or strictly binary tree) is a tree in which every node other than the leaves has two children.
Full Binary Tree:每个非叶结点拥有2个孩子。
¤ 注意点
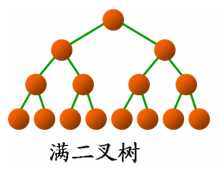
这里Full Binary Tree并不是国内定义的满二叉树,国内定义的满二叉树与下面的Perfect Binary Tree的定义则是一致的。
A complete k-ary tree is a k-ary tree in which all leaves have the same depth and all internal nodes have degree k.
满(这里的complete应该翻译为完整的)k叉树是所有叶节点深度相同,且所有内部结点度为k的k叉树。
A perfect binary tree is a full binary tree in which all leaves are at the same depth or same level, and in which every parent has two children.
满二叉树是一棵full binary tree,它的所有叶子结点深度相同,并且每个父亲结点度为2。