[LeetCode] Sqrt(x)

标签：c++   leetcode   

Sqrt(x)

Implement int sqrt(int x).

Compute and return the square root of x.

解题思路：

这道题是求x的平方根。

解法1：基本的想法就是枚举，从1到n进行遍历，直到result*result>x，那么结果就是result-1。

class Solution {
public:
    int mySqrt(int x) {
        int result = 0;
        while((long long)result * result <= x){
            result++;
        }
        return result - 1;
    }
};

但是这样产生了超时错误。

解法2：采用类似于二分查找的方法，可以在0-x区间内以二分查找的办法找到结果。注意到相乘可能会溢出的情况。

class Solution {
public:
    int mySqrt(int x) {
        long long left = 0, right = x;
        long long middle = (left+right) / 2;
        while(left<right){
            long long temp = middle*middle;
            if(temp == x){
                return middle;
            }else if(temp > x){
                right = middle - 1;
            }else{
                left = middle + 1;
            }
            middle = (left + right) / 2;
        }
        if((long long)middle*middle>(long long)x){
            return (int)middle - 1;
        }else{
            return (int)middle;
        }
    }
};

为了方便理解，就先以本题为例：

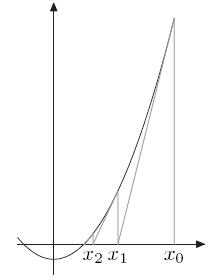
   计算x² = n的解，令f(x)=x²-n，相当于求解f(x)=0的解，如左图所示。

   首先取x₀，如果x₀不是解，做一个经过(x₀,f(x₀))这个点的切线，与x轴的交点为x₁。

   同样的道理，如果x₁不是解，做一个经过(x₁,f(x₁))这个点的切线，与x轴的交点为x₂。

   以此类推。

   以这样的方式得到的x_i会无限趋近于f(x)=0的解。

   判断x_i是否是f(x)=0的解有两种方法：

   一是直接计算f(x_i)的值判断是否为0，二是判断前后两个解x_i和x_i-1是否无限接近。

经过(x_i, f(x_i))这个点的切线方程为f(x) = f(x_i) + f’(x_i)(x - x_i)，其中f‘(x)为f(x)的导数，本题中为2x。令切线方程等于0，即可求出x_i+1=x_i - f(x_i) / f‘(x_i)。

继续化简，x_i+1=x_i - (x_i² - n) / (2x_i) = x_i - x_i / 2 + n / (2x_i) = x_i / 2 + n / 2x_i = (x_i + n/x_i) / 2。

有了迭代公式，程序就好写了。关于牛顿迭代法，可以参考wikipedia以及百度百科。

牛顿迭代法也同样可以用于求解多次方程的解。

P.S. 本题是求解整数的平方根，并且返回值也是整型。在上述代码基础上稍微做修改，就可以同样适用于double（仅限方法2）。

double sqrt(double x) {
    if (x == 0) return 0;
    double last = 0.0;
    double res = 1.0;
    while (res != last)
    {
        last = res;
        res = (res + x / res) / 2;
    }
    return res;
}

[LeetCode] Sqrt(x)

标签：c++   leetcode   

原文地址：http://blog.csdn.net/kangrydotnet/article/details/47091385