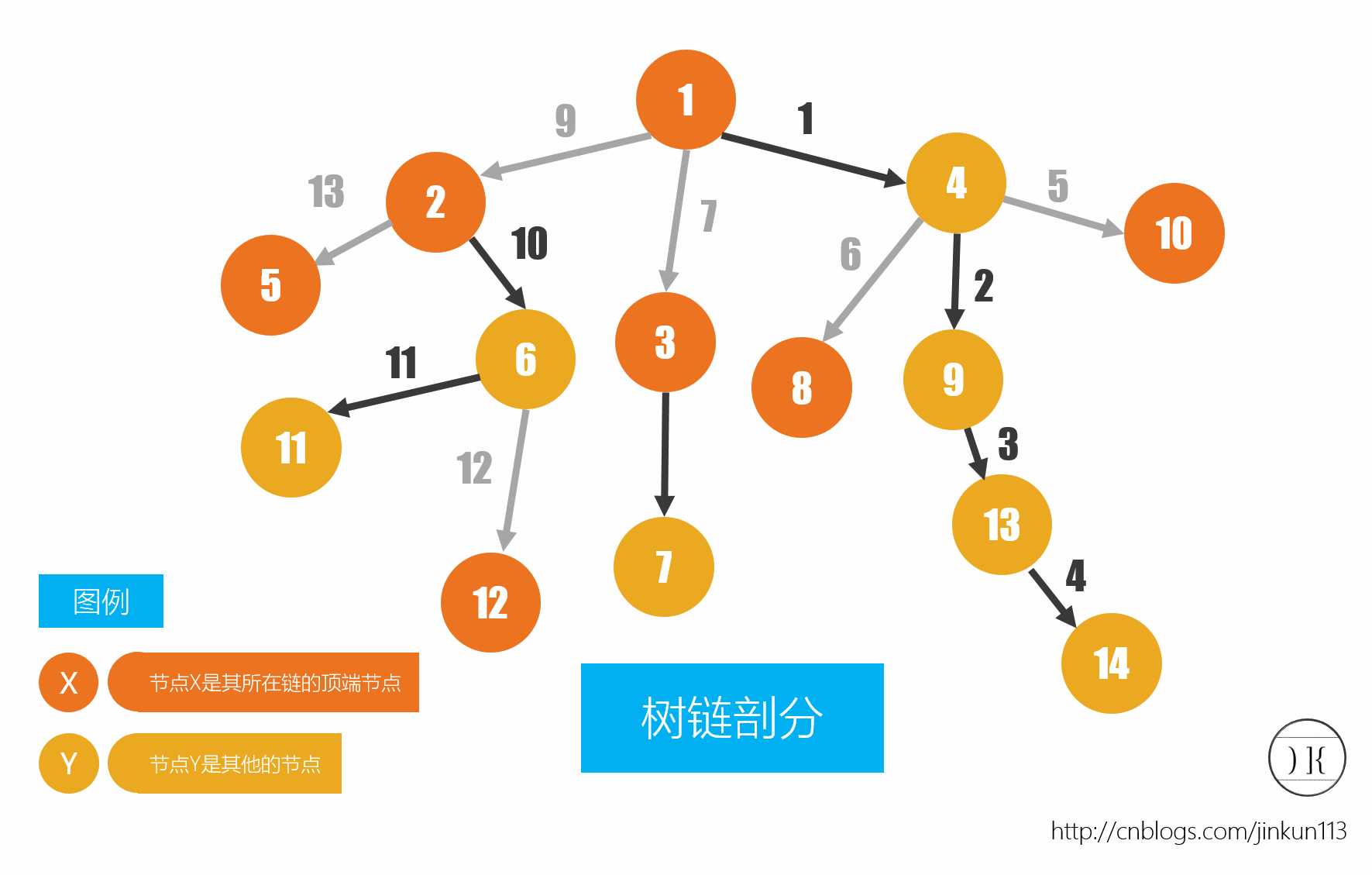
具体实现方面的话,上文所提的重儿子,顶端,深度等等都要提前预处理出来,后面就是用线段树维护了。
----------------------------------------------------------------------------------------------------
#include<cstdio>
#include<algorithm>
#define MAXN 30005
#define INF 1<<30
using namespace std;
int l[MAXN],r[MAXN];
struct node
{
int sum,max;
};
node tree[MAXN*4];
struct Edge
{
int v,next;
};
Edge edge[MAXN*2];
int head[MAXN],now,val[MAXN],link[MAXN],dep[MAXN],fa[MAXN],sonTree[MAXN],heavySon[MAXN],tot,top[MAXN],num[MAXN];
int n,u,v,q;
void addEdge(int u,int v)
{
now++;
edge[now].v=v;
edge[now].next=head[u];
head[u]=now;
}
void buildTree(int now,int l,int r)
{
if (l==r)
{
tree[now].max=val[link[l]];
tree[now].sum=val[link[l]];
return;
}
int mid=(l+r)/2;
buildTree(now*2,l,mid);
buildTree(now*2+1,mid+1,r);
tree[now].max=max(tree[now*2].max,tree[now*2+1].max);
tree[now].sum=tree[now*2].sum+tree[now*2+1].sum;
}
void DFS1(int now,int nowFa,int nowDep)
{
dep[now]=nowDep; fa[now]=nowFa; sonTree[now]=1;
for (int x=head[now];x!=0;x=edge[x].next)
{
if (edge[x].v==nowFa) continue;
DFS1(edge[x].v,now,nowDep+1);
sonTree[now]+=sonTree[edge[x].v];
if (heavySon[now]==0 || sonTree[edge[x].v]>sonTree[heavySon[now]]) heavySon[now]=edge[x].v;
}
}
void DFS2(int now,int nowTop)
{
tot++;
top[now]=nowTop; num[now]=tot; link[tot]=now;
if (heavySon[now]==0) return;
DFS2(heavySon[now],nowTop);
for (int x=head[now];x!=0;x=edge[x].next)
if (edge[x].v!=heavySon[now] && edge[x].v!=fa[now]) DFS2(edge[x].v,edge[x].v);
}
void init()
{
scanf("%d",&n);
for (int i=1;i<=n-1;i++)
{
scanf("%d %d",&u,&v);
addEdge(u,v); addEdge(v,u);
}
for (int i=1;i<=n;i++) scanf("%d",&val[i]);
DFS1(1,0,1); DFS2(1,1);
buildTree(1,1,n);
}
void update1(int now,int l,int r,int loc,int delta)
{
if (l==r)
{
tree[now].sum+=delta;
tree[now].max+=delta;
return;
}
int mid=(l+r)/2;
if (loc<=mid) update1(now*2,l,mid,loc,delta);
else update1(now*2+1,mid+1,r,loc,delta);
tree[now].max=max(tree[now*2].max,tree[now*2+1].max);
tree[now].sum=tree[now*2].sum+tree[now*2+1].sum;
}
int query1(int now,int l,int r,int ql,int qr)
{
int ans=0;
if (ql<=l && r<=qr) return tree[now].sum;
int mid=(l+r)/2;
if (ql<=mid) ans+=query1(now*2,l,mid,ql,qr);
if (qr>mid) ans+=query1(now*2+1,mid+1,r,ql,qr);
return ans;
}
int query2(int now,int l,int r,int ql,int qr)
{
int ans=-INF;
if (ql<=l && r<=qr) return tree[now].max;
int mid=(l+r)/2;
if (ql<=mid) ans=max(ans,query2(now*2,l,mid,ql,qr));
if (qr>mid) ans=max(ans,query2(now*2+1,mid+1,r,ql,qr));
return ans;
}
int getMax(int l,int r)
{
int f1=top[l],f2=top[r],ans=-INF,nowAns;
while (f1!=f2)
{
if (dep[f1]<dep[f2]) swap(f1,f2),swap(l,r);
ans=max(ans,query2(1,1,n,num[f1],num[l]));
l=fa[f1]; f1=top[l];
}
if (dep[l]>dep[r]) nowAns=query2(1,1,n,num[r],num[l]);
else nowAns=query2(1,1,n,num[l],num[r]);
ans=max(ans,nowAns);
return ans;
}
int getSum(int l,int r)
{
int f1=top[l],f2=top[r],ans=0,nowAns;
while (f1!=f2)
{
if (dep[f1]<dep[f2]) swap(f1,f2),swap(l,r);
ans+=query1(1,1,n,num[f1],num[l]);
l=fa[f1]; f1=top[l];
}
if (dep[l]>dep[r]) nowAns=query1(1,1,n,num[r],num[l]);
else nowAns=query1(1,1,n,num[l],num[r]);
ans+=nowAns;
return ans;
}
int main()
{
char s[7];
init();
scanf("%d",&q);
for (int i=1;i<=q;i++)
{
scanf("%s %d %d",s,&u,&v);
if (s[0]==‘C‘) { update1(1,1,n,num[u],v-val[u]); val[u]=v; }
else if (s[1]==‘M‘) printf("%d\n",getMax(u,v));
else printf("%d\n",getSum(u,v));
}
return 0;
}
----------------------------------------------------------------------------------------------------