标签:
连续型变量在一定区间内可以取任何值,因此其概率分布不能以分布列来表示,只能通过概率分布密度曲线表示。
1.正态分布
正态分布是最常见也是最重要的一种连续分布,概率密度函数如下:
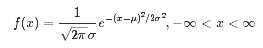
累积概率分布函数如下:
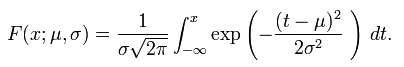
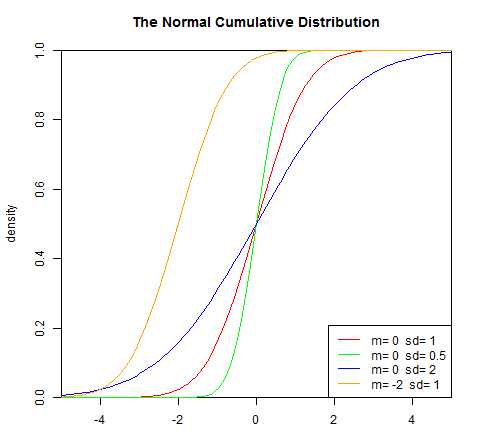
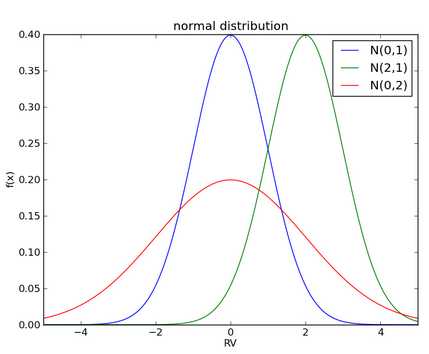
正态分布有两个参数,μ和σ。我们可以将正态分布表示成N(μ,σ)。当μ=0,σ=1,这样的正态分布被称作标准正态分布
2.指数分布
指数分布用来表示独立随机事件发生的时间间隔,其密度函数随着取值的变大而指数减小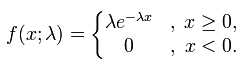
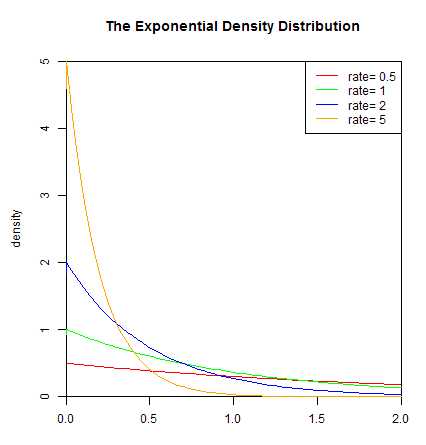
其中λ > 0是分布的一个参数,常被称为率参数(rate parameter)。即每单位时间内发生某事件的次数。指数分布的区间是[0,∞)。 如果一个随机变量X呈指数分布,则可以写作:X~ Exponential(λ)累积概率分布函数如下: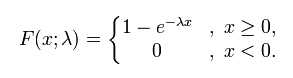
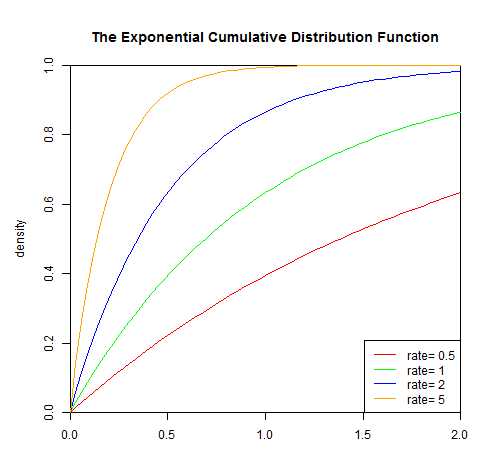
指数分布是伽玛分布和weibull分布的特殊情况,产品的失效是偶然失效时,其寿命服从指数分布。指数分布也可以看作当weibull分布中的形状系数等于1的特殊分布,指数分布的失效率是与时间t无关的常数,所以分布函数简单。
指数函数的一个重要特征是无记忆性(又称遗失记忆性)。这表示如果一个随机变量呈指数分布,当s,t≥0时有P(T>s+t|T>t)=P(T>s),即,如果T是某一元件的寿命,已知元件使用了t小时,它总共使用至少s+t小时的条件概率,与从开始使用时算起它使用至少s小时的概率相等。显然,指数分布的这种特性,与机械零件的疲劳、磨损、腐蚀、蠕变等损伤过程的实际情况是完全矛盾的,它违背了产品损伤累积和老化这一过程。所以,指数分布不能作为机械零件功能参数的分布形式,但是它可以近似地作为高可靠性的复杂部件、机器或系统的失效分布模型,特别是在部件或机器的整机试验中得到广泛的应用。
3.Gamma(伽马)分布
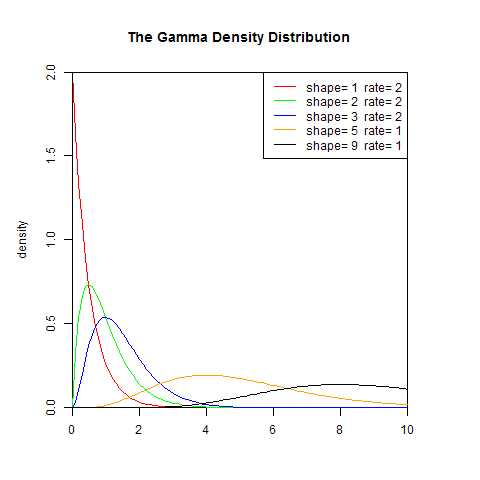
伽玛分布(Gamma)是著名的皮尔逊概率分布函数簇中的重要一员,称为皮尔逊Ⅲ型分布。它的曲线有一个峰,但左右不对称。伽玛分布中的参数α,称为形状参数,β称为尺度参数。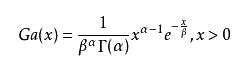
伽马函数为: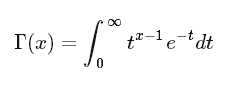
概率密度函数如下: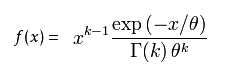
累计分布函数如下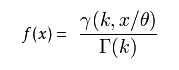
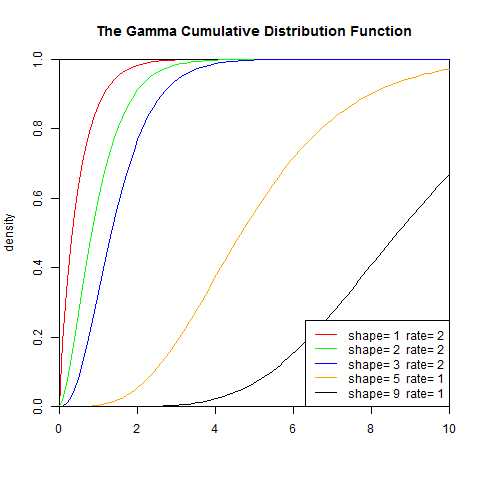
Gamma分布兼有指数分布和幂分布的特点。从Gamma分布公式看,当β为零时,它就变成了幂分布。当n=1时,它变成了指数分布。而它的分布函数是前两种分布的乘积(系数做了调整)。幂分布与指数分布在变量值很小时其概率值很大,但是它们组成的Gamma的最大值却不在变量最小时而是有一个峰值比较居中
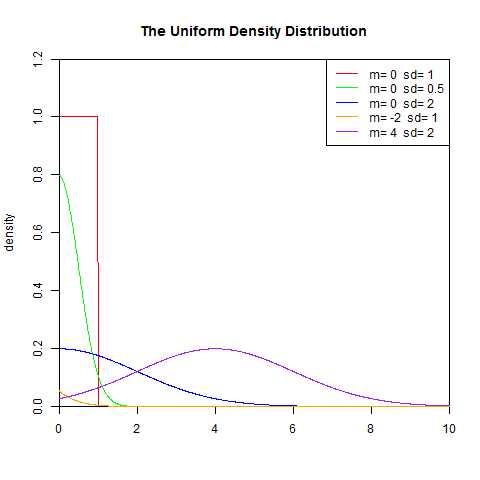
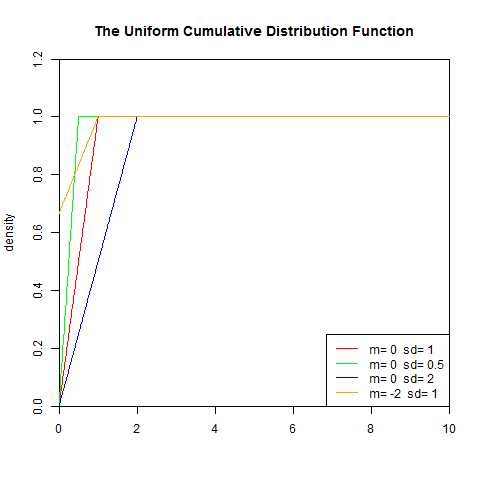
4.均匀分布
均匀分布是均匀的,不偏差的一种简单的概率分布,分为离散型均匀分布和连续型均匀分布,其主要特点是:测量值在某一范围内各处出现的机会一样,即均匀一致,故又称为矩形分布或等概率分布。
概率密度函数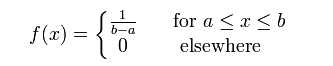
累积分布函数
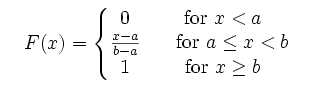
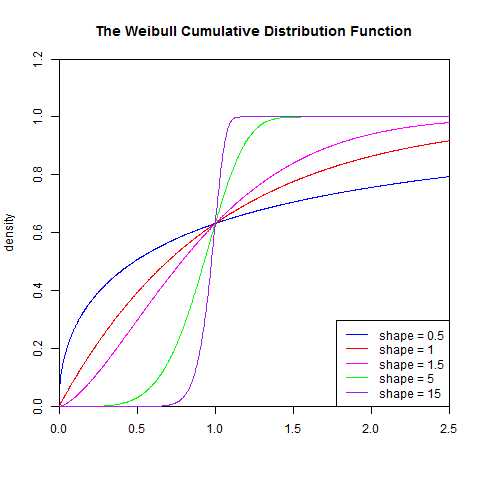
5.weibull分布
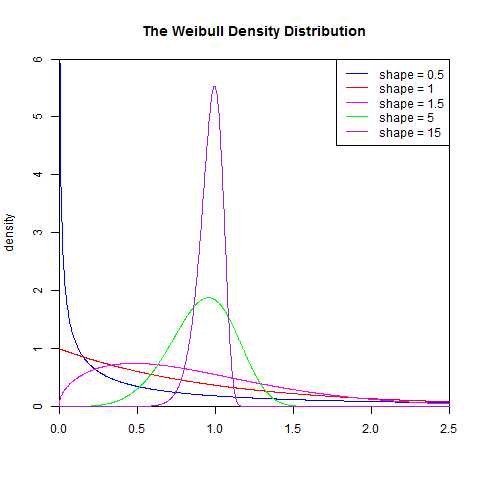
weibull(韦伯)分布,又称韦氏分布或威布尔分布,是可靠性分析和寿命检验的理论基础。Weibull分布能被应用于很多形式,分布由形状、尺度(范围)和位置三个参数决定。其中形状参数k是最重要的参数,决定分布密度曲线的基本形状,尺度参数λ起放大或缩小曲线的作用,但不影响分布的形状。
Weibull分布通常用在故障分析领域( field of failure analysis)中;尤其是它可以模拟(mimic) 故障率(failture rate)持续( over time)变化的分布。
故障率为:
1.一直为常量(constant over time),那么α=1,暗示在随机事件中发生
2.一直减少(decreases over time),那么α<1, 暗示"早期失效(infant mortality)"
3.一直增加(increases over time),那么α>1, 暗示"耗尽(wear out)" - 随着时间的推进,失败的可能性变大
概率密度函数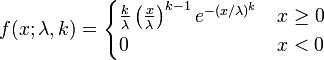
累积分布函数
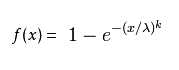
Weibull distribution与很多分布都有关系。如,当k=1,它是指数分布;k=2时,是Rayleigh distribution(瑞利分布)。X是随机变量,是位置参数,这个参数可正可负,通常为正值或等于零,正值表示时间延滞,简称时滞。
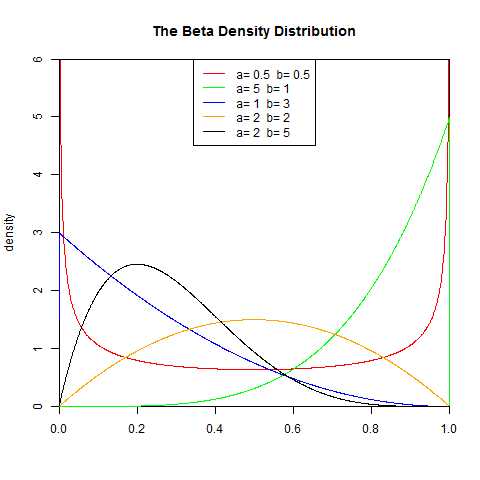
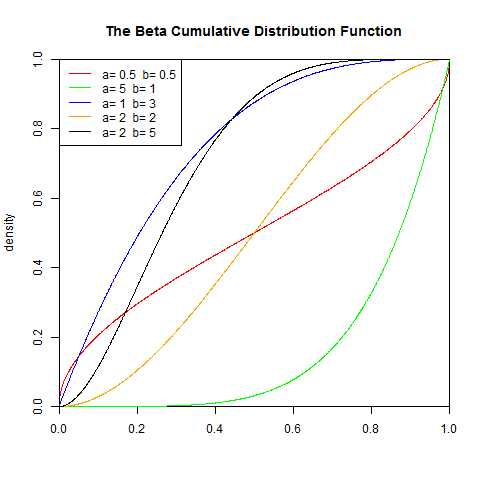
6.β(贝塔Beta)分布
贝塔分布(Beta Distribution)是指一组定义在(0,1)区间的连续概率分布,Beta分布有α和β两个参数α,β>0,其中α为成功次数加1,β为失败次数加1。
Beta分布的一个重要应该是作为伯努利分布和二项式分布的共轭先验分布出现,在机器学习和数理统计学中有重要应用。贝塔分布中的参数可以理解为伪计数,伯努利分布的似然函数可以表示为,表示一次事件发生的概率,它为贝塔有相同的形式,因此可以用贝塔分布作为其先验分布。
概率密度函数

随机变量X服从参数为a, β,服从Beta分布,γ 是伽玛函数
累积分布函数如下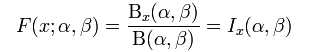
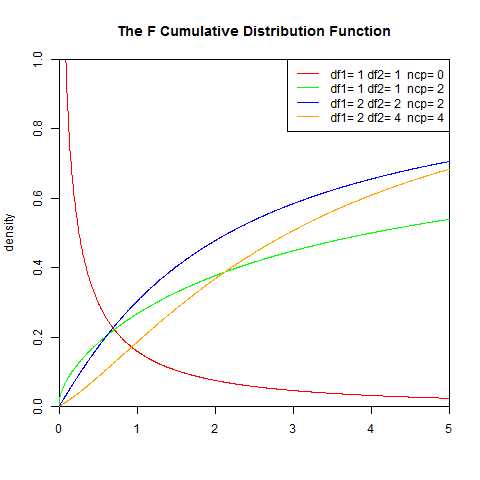
7.F分布
F分布由Fisher提出,被广泛应用于似然比率检验,特别是ANOVA中。F分布定义为:设X、Y为两个独立的随机变量,X服从自由度为k1的卡方分布,Y服从自由度为k2的卡方分布,这2 个独立的卡方分布被各自的自由度除以后的比率这一统计量的分布。即: 上式F服从第一自由度为k1,第二自由度为k2的F分布。
F分布的性质
1.它是一种非对称分布
2.它有两个自由度,即n1 -1和n2-1,相应的分布记为F( n1 –1, n2-1), n1 –1通常称为分子自由度, n2-1通常称为分母自由度
3.F分布是一个以自由度n1 –1和n2-1为参数的分布族,不同的自由度决定了F 分布的形状
4.F分布的倒数性质: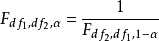
概率密度函数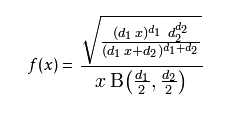
B是Beta函数(beta function)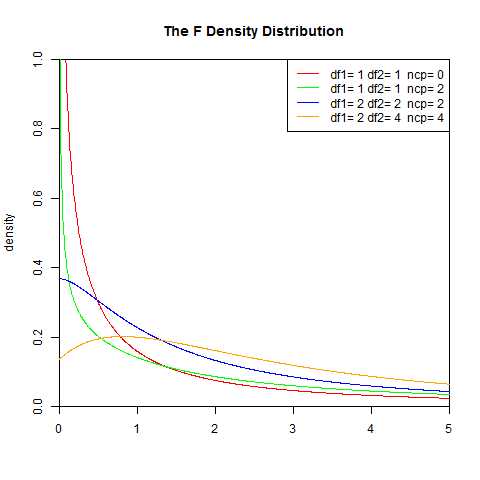
累积分布函数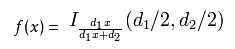
8.T分布
学生t-分布(Student‘s t-distribution),可简称为t分布。应用在估计呈正态分布的母群体之平均数。它是对两个样本均值差异进行显著性测试的学生t检定的基础。学生t检定改进了Z检定(Z-test),因为Z检定以母体标准差已知为前提。虽然在样本数量大(超过30个)时,可以应用Z检定来求得近似值,但Z检定用在小样本会产生很大的误差,因此必须改用学生t检定以求准确。在母体标准差未知的情况下,不论样本数量大或小皆可应用学生t检定。在待比较的数据有三组以上时,因为误差无法压低,此时可以用变异数分析(ANOVA)代替学生t检定。
概率密度函数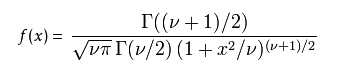
v 等于n-1。 T的分布称为t-分布。参数\nu 一般被称为自由度。
γ 是伽玛函数。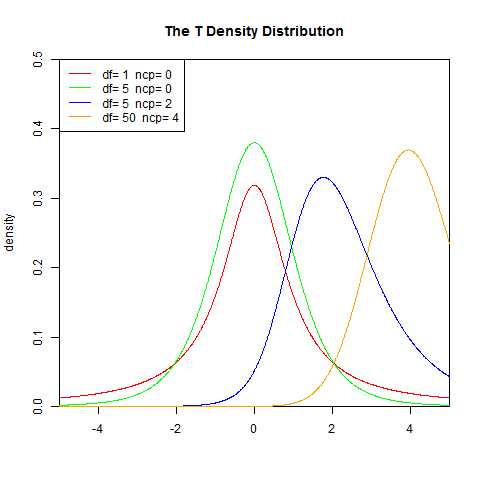
累积分布函数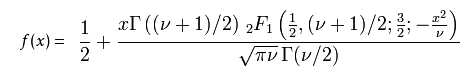
v 等于n-1。 T的分布称为t-分布。参数\nu 一般被称为自由度。
γ 是伽玛函数。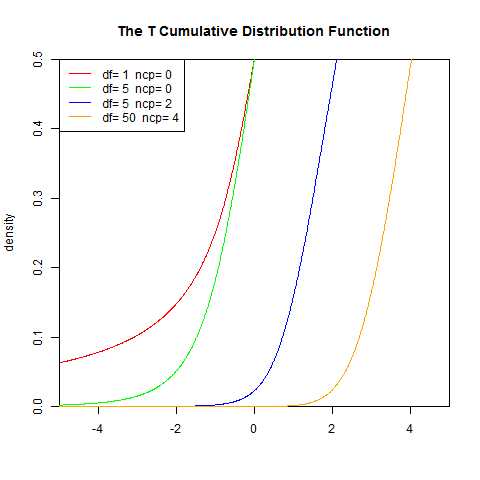
T分布的特点
1.以0为中心,左右对称的单峰分布;
2.t分布曲线形态与n(确切地说与自由度v)大小有关。与标准正态分布曲线相比,自由度v越小,t分布曲线愈平坦,曲线中间愈低,曲线双侧尾部翘得愈高;自由度v愈大,t分布曲线愈接近正态分布曲线,当自由度v=∞时,t分布曲线为标准正态分布曲线。
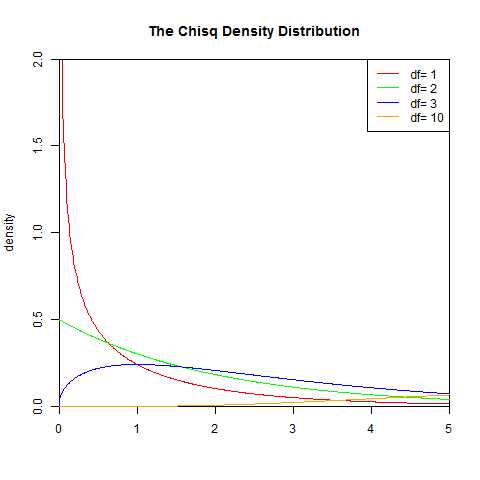
9.χ²(卡方)分布
若n个相互独立的随机变量ξ1、ξ2、……、ξn ,均服从标准正态分布(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为χ²分布(chi-square distribution)。其中参数n称为自由度,自由度不同就是另一个χ²分布,正如正态分布中均值或方差不同就是另一个正态分布一样。
卡方分布是由正态分布构造而成的一个新的分布,当自由度n很大时,分布近似为正态分布。
概率密度函数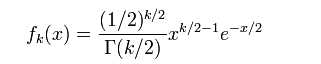
γ 是伽玛函数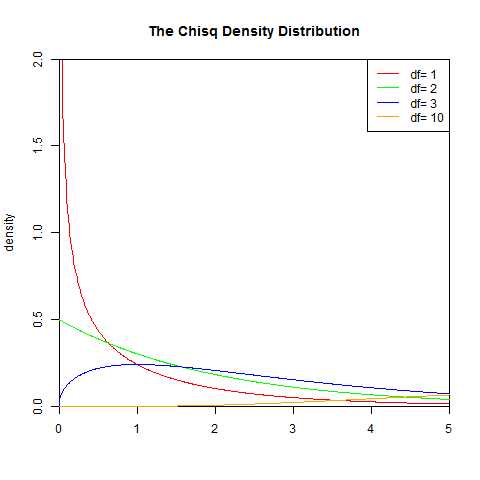
累积分布函数
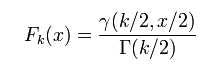
γ 是伽玛函数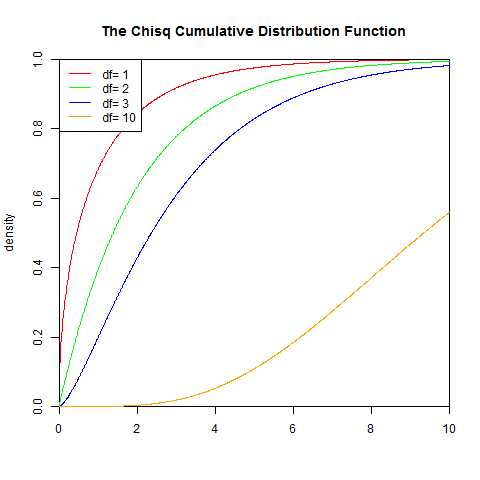
标签:
原文地址:http://www.cnblogs.com/xmdata-analysis/p/4683477.html