标签:
骨牌,一种古老的玩具。今天我们要研究的是骨牌的覆盖问题:
我们有一个2xN的长条形棋盘,然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘,一共有多少种不同的覆盖方法呢?
举个例子,对于长度为1到3的棋盘,我们有下面几种覆盖方式:
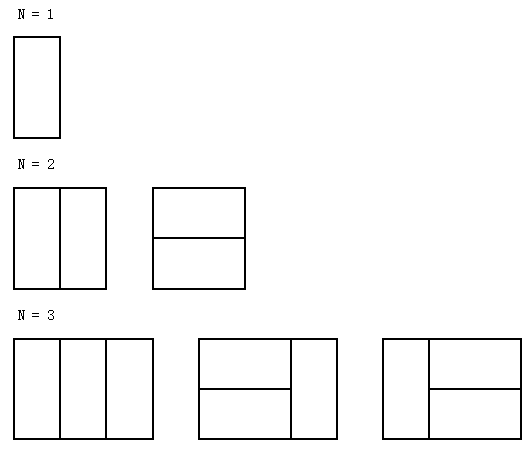
第1行:1个整数N。表示棋盘长度。1≤N≤100,000,000
第1行:1个整数,表示覆盖方案数 MOD 19999997
62247088
17748018
分析:n超大,如果按照递推计算斐波那契第n项相当费时间,线性代数的矩阵有加速运算的效果。
此代码基本可以算作模板,但需要注意一个地方,在上面的这道题目中,f[1]=1,f[2]=2,,,以此类推下去。
但有的序列可能是:1 1 2 3,,,因为有一点不同就需要稍微修改一下矩阵累乘的次数,也就是矩阵的指数。
代码:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <iostream>
#include <string>
#include <vector>
#include <queue>
#include <math.h>
#define eps 1e-8
#include <algorithm>
using namespace std;
//矩阵快速幂运算(矩阵加速运算)
struct matrix{
long long a[2][2]; //定义2x2的矩阵
};
matrix mul(matrix x, matrix y, long mod )
{
matrix ret; //按照矩阵相乘求ret矩阵的每个元素的值 然后返回它
ret.a[0][0]=((x.a[0][0]%mod)*y.a[0][0]%mod + (x.a[0][1]%mod)*y.a[1][0]%mod )%mod;
ret.a[0][1]=((x.a[0][0]%mod)*y.a[0][1]%mod + (x.a[0][1]%mod)*y.a[1][1]%mod )%mod;
ret.a[1][0]=((x.a[1][0]%mod)*y.a[0][0]%mod + (x.a[1][1]%mod)*y.a[1][0]%mod )%mod;
ret.a[1][1]=((x.a[1][0]%mod)*y.a[0][1]%mod + (x.a[1][1]%mod)*y.a[1][1]%mod )%mod;
return ret;
}
//求矩阵x的幂取模,e为指数
matrix mypow(matrix x, long long e, long mod)//(x^e)%mod
{
matrix ret, temp;
if(e==0){
ret.a[0][0]=1; ret.a[0][1]=0;
ret.a[1][0]=0; ret.a[1][1]=1;
return ret;
}
if(e==1) return x; //当指数为1时,返回原来的矩阵
temp=mypow(x, e>>1, mod); //x的 e/2次方
ret=mul(temp, temp, mod); //ret=temp*temp
if(e&1) ret=mul(ret, x, mod); //如果e为奇数,ret乘以x
return ret; //返回答案
}
int main()
{
long n, m=19999997;//m就是mod
matrix ans;
while(scanf("%ld", &n)!=EOF)
{
//矩阵初始化
ans.a[0][0]=1; ans.a[0][1]=1;
ans.a[1][0]=1; ans.a[1][1]=0;
if( n ){
ans = mypow(ans, n, m); //此处的n就是指数(考虑n是否在对应的题目中需要修改), m是取模数
printf("%lld\n", ans.a[0][0]);
}else{
printf("0\n");
}
}
return 0;
}
标签:
原文地址:http://www.cnblogs.com/yspworld/p/4684413.html