标签:
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 10505 | Accepted: 1584 |
Description
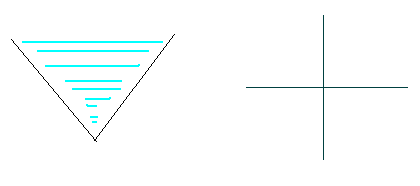
Input
Output
Sample Input
2 0 1 1 0 1 0 2 1 0 1 2 1 1 0 1 2
Sample Output
1.00 0.00
题解:判断可以接多少水,如果两直线可以接水的话,求三角形面积
下面给出一些计算几何最基础的结论(常用)
两向量点乘: a*b*cosO = x1*y1+x2*y2 用来 1 :计算夹角 2:计算投影
两向量叉乘: a*b*sinO = x1*y1-x2*y2 用来 1:计算面积 2:判断点在直线的哪边,右手法则
这个题输出的时候要注意,用G++交题的时候要最后输出ans+eps;
下面是代码:
1 #include <cmath> 2 #include <cstdio> 3 #include <algorithm> 4 using namespace std; 5 6 #define N 105 7 #define eps 1e-6//精度太小会导致出错,精度太大会增加计算量,自己权衡 8 struct point { 9 double x, y; 10 point(){} 11 point(double x, double y):x(x), y(y){} 12 point operator + (const point o) const{ 13 return point(x+o.x, y+o.y); 14 } 15 point operator - (const point o) const{ 16 return point(x-o.x, y-o.y); 17 } 18 19 double operator * (const point o) const{ 20 return x*o.y - o.x*y; 21 } 22 23 double operator ^ (const point o) const{//点乘 24 return x*o.x + y*o.y; 25 } 26 27 point operator * (const double a) const{ 28 return point(a*x, a*y); 29 } 30 31 double len2() 32 { 33 return x*x + y*y; 34 } 35 }a, b, s, t; 36 37 point Intersection(point a, point b, point c, point d) 38 { 39 double t = ((d - a)*(c - a))/((b - a)*(d - c)); 40 return a + (b-a)*fabs(t); 41 } 42 43 int main() 44 { 45 point a, b, c, d; 46 int T; 47 scanf("%d", &T); 48 while(T--) 49 { 50 scanf("%lf %lf %lf %lf", &a.x, &a.y, &b.x, &b.y); 51 scanf("%lf %lf %lf %lf", &c.x, &c.y, &d.x, &d.y); 52 53 if(fabs(a.y - b.y) < eps || fabs(c.y - d.y) < eps)//有水平线 54 { 55 puts("0.00"); 56 continue; 57 } 58 59 if(a.y < b.y) swap(a, b); 60 if(c.y < d.y) swap(c, d); 61 62 if(fabs((b.y-a.y)*(d.x-c.x) - (d.y-c.y)*(b.x-a.x)) < eps) //两条线平行 63 { 64 puts("0.00"); 65 continue; 66 } 67 68 if(((b-a)*(c-a))*((b-a)*(d-a)) > 0 || ((d-c)*(a-c))*((d-c)*(b-c)) > 0)//两条线段根本没有交点 69 { 70 puts("0.00"); 71 continue; 72 } 73 point p = Intersection(a, b, c, d); 74 point up = point(0,10); 75 if(((a-p)*(up)) * ((c-p)*(up)) > 0)//能收集雨水的部分在竖直线的同一侧 76 { 77 if((a-p)*(c-p) > 0 && c.x- a.x>= -eps) 78 { 79 puts("0.00"); 80 continue; 81 } 82 if((a-p)*(c-p) < 0 && a.x- c.x>= -eps) 83 { 84 puts("0.00"); 85 continue; 86 } 87 } 88 point t1, t2; 89 t1.y = t2.y = min(a.y, c.y); 90 t1.x = a.x + (b.x - a.x)*(t1.y - a.y)/(b.y-a.y); 91 t2.x = c.x + (d.x - c.x)*(t2.y - c.y)/(d.y-c.y); 92 double ans = fabs((t1.x - t2.x) * (t1.y-p.y)/2.0); 93 printf("%.2f\n", ans+eps); //控制精度, 94 } 95 return 0; 96 }
An Easy Problem?!(细节题,要把所有情况考虑到)
标签:
原文地址:http://www.cnblogs.com/shanyr/p/4688449.html