标签:
具体文字定义就不多说了,网上有很多,下面给出数学公式描述(有时候会有一些变种,不过都大同小异):
f(0) = 1 , f(1) = 1, f(n) = f(n-1)+f(n-2) n>=2
解决斐波那契问题,大多数人第一反应就是递归,思路简单清晰,代码易实现,不多说了,直接看代码。
1 long long int Fibonacci(int n) 2 { 3 if (n < 2) { 4 return 1; 5 } 6 7 return Fibonacci(n-1) + Fibonacci(n-2); 8 }
以上递归求解存在很严重的问题,不仅效率低下,而且当n稍微大一点,函数调用栈就会被占满,直接导致程序卡死,这是由于直接递归嵌套的函数调用层次太多,我们将代码稍加改动,改成尾递归,就可避免这种情况。代码如下:
1 // num1和num2分别为数列第一和第二个数的值 2 long long int Fibonacci(int n, long long int num1, long long int num2) 3 { 4 if (n == 0) { 5 return num1; 6 } else if (n == 1) { 7 return num2; 8 } 9 10 return Fibonacci(n-1, num2, num1+num2); 11 }
(关于尾递归的概念,这里不做详细解释。)
尾递归之所以效率高并且不会产生函数栈溢出,其原因就是每次递归都是直接进行函数调用返回,不做表达式计算,这样的形式有利于编译器优化为递推,也就是直接循环。若是觉得尾递归不太好写,我们可以直接写递推,代码如下:
1 long long int Fibonacci(int n) 2 { 3 if (n < 2) { 4 return 1; 5 } 6 7 long long int num1 = 1; 8 long long int num2 = 1; 9 for (int i=2; i<=n; ++i) { 10 long long int result = num1+num2; 11 num1 = num2; 12 num2 = result; 13 } 14 15 return num2; 16 }
首先需要知道的是,矩阵乘法可以将大多数可以递推以线性时间解决的问题优化到O(logN)的时间复杂度。这里不再讲解数学推理(因为本人也懒得研究),直接上结论:
根据数学推理,可将f(n) = f(n-1) + f(n-2)转换为以下形式:
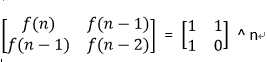
以上情况在n >= 2时成立。
因此,如果要求得f(n),只需要求公式右边矩阵的n次方,就可以得到结果,这样问题就转化为了矩阵乘方问题。
但如果从1到n循环做乘法,效率还是没有优化,这是我们可以根据乘方的特点来进行优化,如下:
an = an/2*an/2a (n为偶数)
an = an/2*an/2*a (n为奇数)
根据上面规律,要求得a的n次方,只需要求出a的n/2次方,然后再做一次乘法即可得到结果,这样我们就将时间复杂度优化到O(logN)。
这是本人第一次看到有次解法,代码参考了其他网友的思路:
1 // 矩阵结构体 2 struct Matrix 3 { 4 Matrix( 5 long long int m00, 6 long long int m01, 7 long long int m10, 8 long long int m11 9 ) 10 11 :M00(m00), M01(m01), M10(m10), M11(m11) 12 { 13 } 14 15 long long int M00; 16 long long int M01; 17 long long int M10; 18 long long int M11; 19 }; 20 21 // 两矩阵相乘 22 Matrix MatrixMultiply(Matrix matrixA, Matrix matrixB) 23 { 24 Matrix matrixTmp(0, 0, 0, 0); 25 26 matrixTmp.M00 = matrixA.M00*matrixB.M00 + matrixA.M01*matrixB.M10; 27 matrixTmp.M01 = matrixA.M00*matrixB.M01 + matrixA.M01*matrixB.M11; 28 matrixTmp.M10 = matrixA.M10*matrixB.M00 + matrixA.M11*matrixB.M10; 29 matrixTmp.M11 = matrixA.M10*matrixB.M01 + matrixA.M11*matrixB.M11; 30 31 return matrixTmp; 32 } 33 34 //矩阵乘方 35 Matrix MatrixPower(int n) 36 { 37 if (n < 2) { 38 return Matrix(1, 1, 1, 0); 39 } 40 41 Matrix matrixTmp(1, 1, 1, 0); 42 43 if (n % 2 == 0) { 44 matrixTmp = MatrixPower(n/2); 45 return MatrixMultiply(matrixTmp, matrixTmp); 46 } else { 47 matrixTmp = MatrixPower(n/2); 48 return MatrixMultiply(MatrixMultiply(matrixTmp, matrixTmp), Matrix(1, 1, 1, 0)); 49 } 50 } 51 52 // 计算斐波那契 53 long long int Fibonacci(int n) 54 { 55 if (n < 2) { 56 return 1; 57 } 58 59 Matrix matrix = MatrixPower(n); 60 61 return matrix.M00; 62 }
标签:
原文地址:http://www.cnblogs.com/mhscn/p/4689501.html