标签:
这道题前2行的输出比较容易,就是简单的动态规划,然后第3行就是比较少见的有上下界的最小流。
前2行比较容易,我们讨论一下第3行的解法吧。
比如第1个样例:
我们先找出那些可能成为最优解的非平行边:
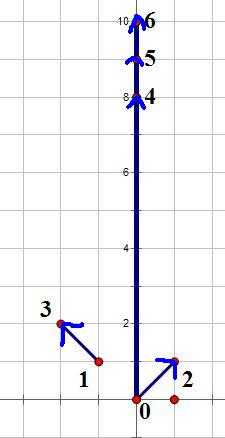
Case11~14做法:
这里保证存在一种最优解,使得轧路机不重复经过同一路面。
我们求出每个点i的入度in[i]和出度out[i]。
然后就是∑max(in[i]-out[i],0)。
我们可以这样想,
当in[i]>out[i]时,必定有in[i]-out[i]条路径在i号点结束。
当in[i]<=out[i]时,一定不会有路径在i号点结束。
其实就是统计在每个点结束的路径个数。
好神奇。。。。。。
100%做法:
其实就是设源点S和汇点T,源点S向所有点连一条下界为0,上界为+oo的边;所有点向汇点T连一条下界为0,上界为+oo的边;原图中边为下界为1,上界为+oo的边,然后求S到T的最小流。
其实就是这样(不妨用(a,b)表示边的下界为a,上界为b):
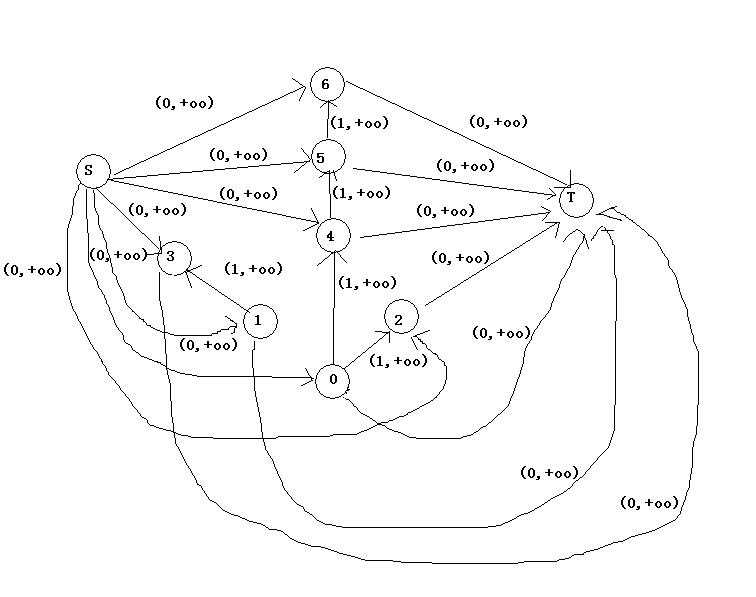 (图丑勿喷)
(图丑勿喷)
然后求有上下界的最小流。
求有上下界的最小流的做法是:
建立superS和superT;
in[i]表示i号点入边的下界和。
out[i]表示i号点出边的下界和。
superS连向每个点i一条容量为in[i]的边;每个点i连向superT一条容量为out[i]边;
原图的边的容量变成为上界-下界。
先不连S到T,求superS到superT的最大流。然后再连S到T一条容量为INF的边,再求supperS到superT的最大流,如果满流,则第二次增广的就是原图的最小流,其实就是满流减去第一次做的最大流。否则无解。
但这道题是肯定有解的,所以不用第二次增广,直接满流-第一次增广得到的最大流。

#include<cstdio> #include<cstdlib> #include<iostream> #include<fstream> #include<algorithm> #include<cstring> #include<string> #include<cmath> #include<queue> #include<stack> #include<map> #include<utility> #include<set> #include<bitset> #include<vector> #include<functional> #include<deque> #include<cctype> #include<climits> #include<complex> //#include<bits/stdc++.h>适用于CF,UOJ,但不适用于poj using namespace std; typedef long long LL; typedef double DB; typedef pair<int,int> PII; typedef complex<DB> CP; #define mmst(a,v) memset(a,v,sizeof(a)) #define mmcy(a,b) memcpy(a,b,sizeof(a)) #define re(i,a,b) for(i=a;i<=b;i++) #define red(i,a,b) for(i=a;i>=b;i--) #define fi first #define se second #define m_p(a,b) make_pair(a,b) #define SF scanf #define PF printf #define two(k) (1<<(k)) template<class T>inline T sqr(T x){return x*x;} template<class T>inline void upmin(T &t,T tmp){if(t>tmp)t=tmp;} template<class T>inline void upmax(T &t,T tmp){if(t<tmp)t=tmp;} const DB EPS=1e-9; inline int sgn(DB x){if(abs(x)<EPS)return 0;return(x>0)?1:-1;} const DB Pi=acos(-1.0); inline void clear(vector<int> *A,int a,int b){int i,j;A->clear();re(i,0,a)re(j,0,b)A[i].push_back(0);} inline int gint() { int res=0;bool neg=0;char z; for(z=getchar();z!=EOF && z!=‘-‘ && !isdigit(z);z=getchar()); if(z==EOF)return 0; if(z==‘-‘){neg=1;z=getchar();} for(;z!=EOF && isdigit(z);res=res*10+z-‘0‘,z=getchar()); return (neg)?-res:res; } inline LL gll() { LL res=0;bool neg=0;char z; for(z=getchar();z!=EOF && z!=‘-‘ && !isdigit(z);z=getchar()); if(z==EOF)return 0; if(z==‘-‘){neg=1;z=getchar();} for(;z!=EOF && isdigit(z);res=res*10+z-‘0‘,z=getchar()); return (neg)?-res:res; } const int maxN=50000; const int INF=1<<30; int N; struct Tpoint{int x,y,id;}p[maxN+100]; int pos[maxN+100]; PII lr[maxN+100]; inline bool cmp1(Tpoint a,Tpoint b){return (a.y!=b.y)?a.y>b.y:a.x<b.x;} inline bool cmp2(Tpoint a,Tpoint b){return (a.x!=b.x)?a.x<b.x:a.y>b.y;} inline bool cmp3(Tpoint a,Tpoint b){return (a.y-a.x!=b.y-b.x)?a.y-a.x<b.y-b.x:a.x>b.x;} inline bool cmp4(Tpoint a,Tpoint b){return (a.y+a.x!=b.y+b.x)?a.y+a.x<b.y+b.x:a.x<b.x;} int now,first[maxN+100]; struct Tedge{int v,next;}edge[3*maxN+100]; inline void addedge(int u,int v) { now++; edge[now].v=v; edge[now].next=first[u]; first[u]=now; } int G[maxN+100],F[maxN+100]; int toG[maxN+100],toF[maxN+100]; int isonlyG[maxN+100],isonlyF[maxN+100]; inline int walk(int head,int tail,int st,int en) { if(st==en) return 0; if(st<en) return en-head; if(st>en) return tail-en; } inline void outputpoint(int x){if(x!=1)PF("%d ",x-1);} inline void outputwalk(int head,int tail,int st,int en) { int x; if(st==en) { outputpoint(p[st].id); return; } if(st<en) { for(x=st;x!=head;x--)outputpoint(p[x].id); outputpoint(p[x].id); for(x=st+1;x!=en;x++)outputpoint(p[x].id); outputpoint(p[x].id); return; } if(st>en) { for(x=st;x!=tail;x++)outputpoint(p[x].id); outputpoint(p[x].id); for(x=st-1;x!=en;x--)outputpoint(p[x].id); outputpoint(p[x].id); return; } } inline void outputway() { int u=1,v; while(u!=-1) { v=toF[u]; outputwalk(lr[pos[u]].fi,lr[pos[u]].se,pos[u],pos[v]); u=toG[v]; } PF("\n"); } int flagF[maxN+100],flagG[maxN+100]; vector<int> V[maxN+100]; int S,T,superS,superT; int intot[maxN+100],outtot[maxN+100]; int tol,info[maxN+100]; struct Tedge2{int v,flow,next;}E[10000000]; inline void addedge2(int u,int v,int flow) { tol++; E[tol].v=v; E[tol].flow=flow; E[tol].next=info[u]; info[u]=tol; } inline void Flow_build() { int i,j; S=N+1;T=N+2;superS=N+3;superT=N+4; mmst(info,-1);tol=-1; re(i,1,N)re(j,0,int(V[i].size())-1)outtot[i]++,intot[V[i][j]]++; re(i,1,N+2) { addedge2(superS,i,intot[i]);addedge2(i,superS,0); addedge2(i,superT,outtot[i]);addedge2(superT,i,0); } re(i,1,N) addedge2(S,i,INF),addedge2(i,S,0); re(i,1,N) addedge2(i,T,INF),addedge2(T,i,0); re(i,1,N)re(j,0,int(V[i].size())-1) addedge2(i,V[i][j],INF),addedge2(V[i][j],i,0); } int level[maxN+100],last[maxN+100]; int head,tail,que[maxN+100]; inline int Dinic_Build() { int i; mmst(level,0); level[que[head=tail=1]=superS]=1; while(head<=tail) { int u=que[head++],v,flow; for(i=info[u],v=E[i].v,flow=E[i].flow;i!=-1;i=E[i].next,v=E[i].v,flow=E[i].flow) if(!level[v] && flow>0)level[que[++tail]=v]=level[u]+1; } return level[superT]; } inline int Dinic(int u,int delta) { if(u==superT) return delta; int res=0,&i=last[u],v,flow; for(v=E[i].v,flow=E[i].flow;i!=-1;i=E[i].next,v=E[i].v,flow=E[i].flow) if(level[u]+1==level[v] && flow>0) { int tmp=Dinic(v,min(delta,flow)); delta-=tmp; res+=tmp; E[i].flow-=tmp; E[i^1].flow+=tmp; if(delta==0) return res; } return res; } inline int check() { int u=1; while(u!=-1) { if(!isonlyF[u])return 0; u=toF[u]; if(!isonlyG[u])return 0; u=toG[u]; } int cnt=0,f=0; u=1; while(u!=-1) { if(toF[u]!=u) f=0; u=toF[u]; if(toG[u]==-1)break; if(!f){cnt++;f=1;} u=toG[u]; } PF("%d\n",cnt); return 1; } int main() { freopen("farm.in","r",stdin); freopen("farm.out","w",stdout); int i,j,k; N=gint()+1; p[1].x=0,p[1].y=0,p[1].id=1; re(i,2,N)p[i].x=gint(),p[i].y=gint(),p[i].id=i; mmst(first,-1);now=-1; sort(p+1,p+N+1,cmp2); re(i,2,N)if(p[i].x==p[i-1].x)addedge(p[i].id,p[i-1].id); sort(p+1,p+N+1,cmp3); re(i,2,N) if(p[i].y-p[i].x==p[i-1].y-p[i-1].x) addedge(p[i].id,p[i-1].id); sort(p+1,p+N+1,cmp4); re(i,2,N)if(p[i].y+p[i].x==p[i-1].y+p[i-1].x)addedge(p[i].id,p[i-1].id); sort(p+1,p+N+1,cmp1); re(i,1,N)pos[p[i].id]=i; int head,tail; for(head=1;head<=N;head=tail+1) { for(tail=head;tail+1<=N && p[tail+1].y==p[head].y;tail++); re(j,head,tail)lr[j]=PII(head,tail); re(j,head,tail) { int u=p[j].id,v; G[u]=1;toG[u]=-1;isonlyG[u]=1; for(i=first[u],v=edge[i].v;i!=-1;i=edge[i].next,v=edge[i].v) if(F[v]+1>G[u]) G[u]=F[v]+1,toG[u]=v,isonlyG[u]=1; else if(F[v]+1==G[u]) isonlyG[u]=0; F[u]=G[u],toF[u]=u,isonlyF[u]=1; } /*re(j,head,tail) { int u=p[j].id; F[u]=G[u];toF[u]=u; re(k,head,tail) { int v=p[k].id,dis=walk(head,tail,j,k); if(G[v]+dis>F[u])F[u]=G[v]+dis,toF[u]=v; } }*/ int t=0,tot=0,isonly=1; re(j,head+1,tail) { int u=p[j].id,v=p[j-1].id; if(G[v]+tail-(j-1)>t) t=G[v]+tail-(j-1),tot=v,isonly=1; else if(G[v]+tail-(j-1)==t) isonly=0; if(t>F[u]) F[u]=t,toF[u]=tot,isonlyF[u]=isonly; else if(t==F[u]) if(isonly==0) isonlyF[u]=0; } t=0,tot=0,isonly=1; red(j,tail-1,head) { int u=p[j].id,v=p[j+1].id; if(G[v]+j+1-head>t) t=G[v]+j+1-head,tot=v,isonly=1; else if(G[v]+j+1-head==t) isonly=0; if(t>F[u]) F[u]=t,toF[u]=tot,isonlyF[u]=isonly; else if(t==F[u]) if(isonly==0) isonlyF[u]=0; } } cout<<F[1]-1<<endl; outputway(); if(check())return 0; mmst(flagG,0);mmst(flagF,0); flagF[1]=1; for(tail=N;tail>=1;tail=head-1) { for(head=tail;head-1>=1 && p[head-1].y==p[tail].y;head--); re(j,head,tail)if(flagF[p[j].id]) { int u=p[j].id; re(k,head,tail) { int v=p[k].id,dis=walk(head,tail,j,k); if(G[v]+dis==F[u])flagG[v]=1; } } re(j,head,tail)if(flagG[p[j].id]) { int u=p[j].id,v; for(i=first[u],v=edge[i].v;i!=-1;i=edge[i].next,v=edge[i].v) if(F[v]+1==G[u]) V[u].push_back(v),flagF[v]=1; } } Flow_build(); int fullflow=0,maxflow=0,v,flow; for(i=info[superS],v=E[i].v,flow=E[i].flow;i!=-1;i=E[i].next,v=E[i].v,flow=E[i].flow)fullflow+=flow; while(Dinic_Build()) { re(i,1,N+4)last[i]=info[i]; maxflow+=Dinic(superS,INF); } cout<<fullflow-maxflow<<endl; return 0; }
标签:
原文地址:http://www.cnblogs.com/maijing/p/4689740.html