标签:
1、前言
这是很重要的一个部分,其实之前很多内容均有所提及,今天把许多知识点放在一起讲,也是起一个总结的作用。
2、概念
最近公共祖先,英文简称为LCA,当且仅当存在于树之中。如假设你生了一对双胞胎,那么两门两个人的最近公共祖先就是你了。公共祖先存在很多,但是最近有且仅有一个。如图所示,ans节点就是点x和点y的LCA。
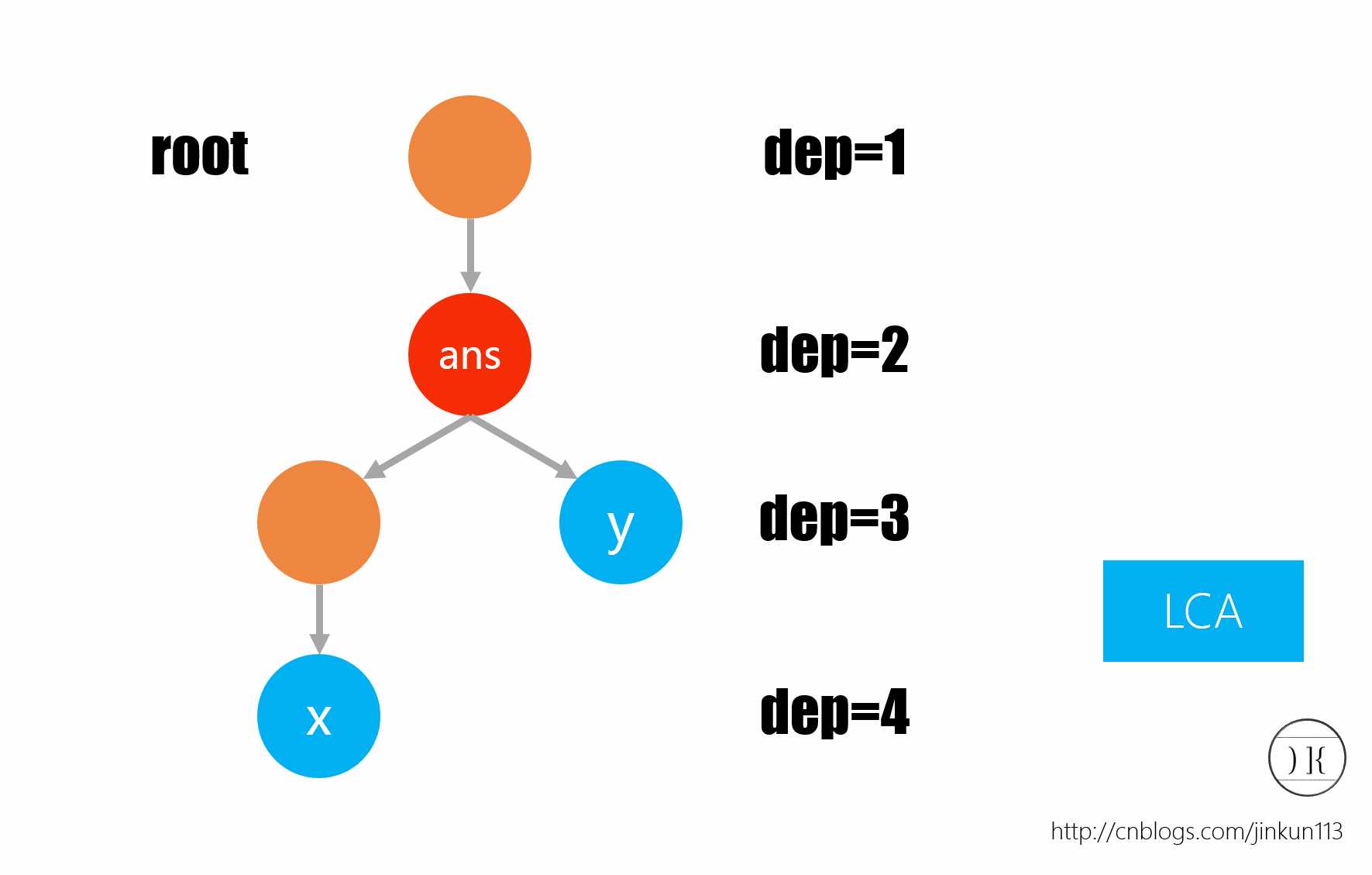
我们很多时候都需要求得LCA,如当对树上点x到点y路径进行一些操作时,首先我们要找到LCA才能得到他们的路径。求LCA的方式有很多,但是大同小异,都是向父亲节点转移。现在根据复杂度一层层来分析。
3、暴力枚举求LCA
很简单的一种方式,但是也是复杂度最高的办法。对于查询点x和点y的LCA,首先根据两点的深度,若dep[x]>dep[y],则点x向父亲节点一步步转移x=fa[x],直到dep[x]=dep[y];反之亦然。当深度相同后,则同时向上转移,即x=fa[x],y=fa[y],直到x=y,此时找到LCA,退出循环。
其基本框架就是递归,时间复杂度为O(max(dep[x],dep[y]))。
4、倍增求LCA
(暂缺)
5、Tarjan求LCA
(暂缺)
6、树链剖分求LCA
之前在单独讲解树链剖分的时候,就已经体现出了它的这一特性。我们为什么要划出重链?划出重链之后为什么要用线段树来维护每一条边?其作用就在于重边总是相连,当得知每条重链的顶端之后,我们向上跑LCA就是简单的一步步爬了,在最优情况下,可以做到O(1)。然而具体实现的话,大家可以参照“树链剖分”专题(),
标签:
原文地址:http://www.cnblogs.com/jinkun113/p/4693327.html