hihoCoder_#1185_连通性·三·强连通分量

标签：acm   algorithm   hihocoder   graphs   tarjan   

描述

暑假到了!!小Hi和小Ho为了体验生活，来到了住在大草原的约翰家。今天一大早，约翰因为有事要出去，就拜托小Hi和小Ho忙帮放牧。

约翰家一共有N个草场，每个草场有容量为W[i]的牧草，N个草场之间有M条单向的路径。

小Hi和小Ho需要将牛羊群赶到草场上，当他们吃完一个草场牧草后，继续前往其他草场。当没有可以到达的草场或是能够到达的草场都已经被吃光了之后，小hi和小Ho就把牛羊群赶回家。

一开始小Hi和小Ho在1号草场，在回家之前，牛羊群最多能吃掉多少牧草？

举个例子：

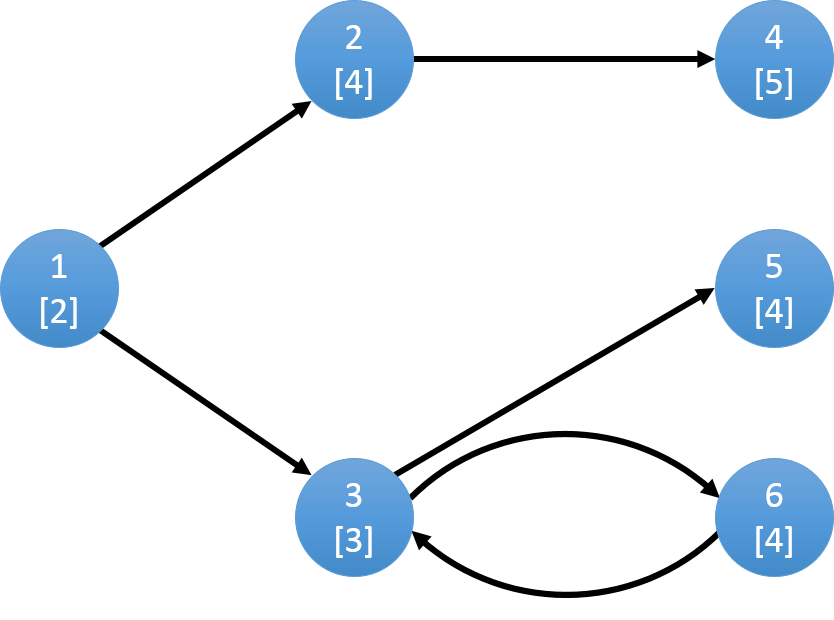
图中每个点表示一个草场，上部分数字表示编号，下部分表示草场的牧草数量w。

在1吃完草之后，小Hi和小Ho可以选择把牛羊群赶到2或者3，假设小Hi和小Ho把牛羊群赶到2：

吃完草场2之后，只能到草场4，当4吃完后没有可以到达的草场，所以小Hi和小Ho就把牛羊群赶回家。

若选择从1到3，则可以到达5，6：

选择5的话，吃完之后只能直接回家。若选择6，还可以再通过6回到3，再到5。

所以该图可以选择的路线有3条：

1->2->4 		total: 11
1->3->5 		total: 9
1->3->6->3->5: 		total: 13
  

所以最多能够吃到的牧草数量为13。

本题改编自USACO月赛金组

提示：强连通分量

输入

第1行：2个正整数，N,M。表示点的数量N，边的数量M。1≤N≤20,000, 1≤M≤100,000

第2行：N个正整数，第i个整数表示第i个牧场的草量w[i]。1≤w[i]≤100,000

第3..M+2行：2个正整数，u,v。表示存在一条从u到v的单向路径。1≤u,v≤N

输出

第1行：1个整数，最多能够吃到的牧草数量。

样例输入

6 6
2 4 3 5 4 4
1 2
2 4
1 3
3 5
3 6
6 3

13

分析：强连通分量缩点后建立新图。然后dfs跑一遍即可。

题目链接：http://hihocoder.com/problemset/problem/1185

代码清单：

#include<map>
#include<set>
#include<queue>
#include<stack>
#include<cmath>
#include<cstdio>
#include<string>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;

const int maxn = 20000 + 5;
const int maxv = 100000 + 5;


int N,M;
int w[maxn];
pair<int,int>edge[maxv];
vector<int>graph[maxn];
vector<int>regraph[maxn];
int dfn[maxn];
int low[maxn];
stack<int>sta;
bool InStack[maxn];
int belong[maxn];
int weight[maxn];
bool vis[maxn];
int idx,sccno,ans;

void init(){
    for(int i=0;i<maxn;i++){
        graph[i].clear();
        regraph[i].clear();
    }
    while(!sta.empty()) sta.pop();
    memset(dfn,0,sizeof(dfn));
    memset(low,0,sizeof(low));
    memset(weight,0,sizeof(weight));
    memset(belong,0,sizeof(belong));
    memset(vis,false,sizeof(vis));
    memset(InStack,false,sizeof(InStack));
    idx=0; sccno=0; ans=0;
}

void input(){
    scanf("%d%d",&N,&M);
    for(int i=1;i<=N;i++)
        scanf("%d",&w[i]);
    for(int i=0;i<M;i++){
        scanf("%d%d",&edge[i].first,&edge[i].second);
        graph[edge[i].first].push_back(edge[i].second);
    }
}

void tarjan(int u){
    low[u]=dfn[u]=++idx;
    InStack[u]=true;
    sta.push(u);
    for(int i=0;i<graph[u].size();i++){
        int v=graph[u][i];
        if(!dfn[v]){
            tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        if(InStack[v]){
            low[u]=min(low[u],dfn[v]);
        }
    }
    if(low[u]==dfn[u]){
        sccno++;
        while(!sta.empty()){
            int j=sta.top();
            sta.pop();
            InStack[j]=false;
            belong[j]=sccno;
            weight[sccno]+=w[j];
            if(j==u) break;
        }
    }
}

void new_graph(){
    for(int i=0;i<M;i++){
        int u=belong[edge[i].first];
        int v=belong[edge[i].second];
        if(u==0||v==0) continue; //点1出发不能到达的点不需进入新图
        if(u!=v)
            regraph[u].push_back(v);
    }
}

void dfs(int u,int sum){
    ans=max(ans,sum);
    for(int i=0;i<regraph[u].size();i++){
        int v=regraph[u][i];
        if(!vis[v]){
            vis[v]=true;
            dfs(v,sum+weight[v]);
            vis[v]=false;
        }
    }
}

void solve(){
//    for(int i=1;i<=N;i++){
//        if(!dfn[i]) tarjan(i);
//    }
    tarjan(1);
    new_graph();
    dfs(belong[1],weight[belong[1]]);
    printf("%d\n",ans);
}

int main(){
    init();
    input();
    solve();
    return 0;
}

hihoCoder_#1185_连通性·三·强连通分量

标签：acm   algorithm   hihocoder   graphs   tarjan   

原文地址：http://blog.csdn.net/jhgkjhg_ugtdk77/article/details/47176669