A binary tree is a finite set of vertices that is either empty or consists of a root r and two disjoint binary trees called the left and right subtrees. There are three most important ways in which the vertices of a binary tree can be systematically traversed or ordered. They are preorder, inorder and postorder. Let T be a binary tree with root r and subtrees T1,T2.

In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.

In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.

In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.

Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.

The input contains several test cases. The first line of each test case contains a single integer n (1<=n<=1000), the number of vertices of the binary tree. Followed by two lines, respectively indicating the preorder sequence and inorder sequence. You can assume they are always correspond to a exclusive binary tree.

For each test case print a single line specifying the corresponding postorder sequence.

9
1 2 4 7 3 5 8 9 6
4 7 2 1 8 5 9 3 6

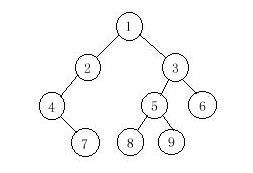
7 4 2 8 9 5 6 3 1	

由二叉树的前序遍历和中序遍历，求后序遍历
大概思路就是：在中序里找前序第一个pre[0]，找到的位置i即为根节点，那么中序里[0,i-1]即是左子树，[i+1,n-1]即为右子树（n为中序序列的长度，下标从0开始的），同时前序的第一个元素（即根节点）就没用了，因为根节点已经构造出来了，那么就从pre[1]开始把前序序列pre分成两部分，怎么分呢？就是前半部分的长度和[0,i-1]长度相等，后半部分和[i+1,l-1]长度相等，然后这就有了两对分半的前序序列和后序序列，然后用这两对分别左右递归构造左右子树。
注意：每次分的前序和中序序列都必须保证长度相等！

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <algorithm>
using namespace std;

int pre[1100],mid[1100],n;

typedef struct Node{
    int v;
    struct Node *left,*right;
}node;

node* root;

node* newNode(int x){
    node* u=(node*)malloc(sizeof(node));
    u->left=u->right=NULL;
    u->v=x;
    return u;
}

node* creat(int *pre,int l1,int *mid,int l2){
    int i,j,k;
    for(i=0;i<l2;i++)
        if(pre[0]==mid[i]) break;
    node* u=newNode(mid[i]);
    if(i>0)
        u->left=creat(pre+1,i,mid,i);       //重点理解这两个if就好了
    if(i<l2-1)
        u->right=creat(pre+i+1,l2-i-1,mid+i+1,l2-i-1);
    return u;
}

void remove_tree(node* u){
    if(u==NULL) return ;
    remove_tree(u->left);
    remove_tree(u->right);
    delete u;
}

int f;

void print(node* u){
    if(u==NULL) return ;
    print(u->left);
    print(u->right);
    if(f)
        printf(" ");
    f=1;
    printf("%d",u->v);
}

int main()
{
    int i,j,n;
    while(scanf("%d",&n)!=EOF){
        for(i=0;i<n;i++)
            scanf("%d",&pre[i]);
        for(i=0;i<n;i++)
            scanf("%d",&mid[i]);
        remove_tree(root);
        root=creat(pre,n,mid,n);
        f=0;
        print(root);
        printf("\n");
    }
    return 0;
}


注意要养成释放空间的好习惯！
POJ2255和这个题基本一样
POJ2255