标签:
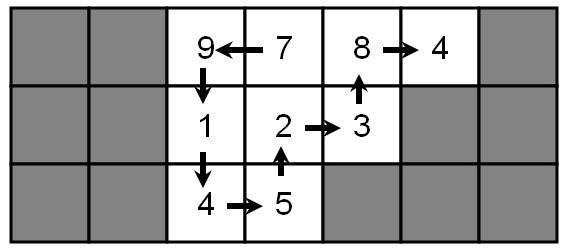
题意
给出如图案例,要你从某一点开始走,一直走到极限(即无法再进行扩展),这时你走过的点会连成一个数,不同的走法当然会有不同的数,要求是输出最大的数(注意每个方块走过一次就不能再走)
思路
所以,需要优化剪枝
Dfs的过程就是构建和遍历解答树的过程,在进行深度优先搜索时有一些分叉是可以判断出无需遍历的,这时就可以把这一部分跳过,continue掉
剪枝: 首先一个数它与另一个数最大的区别在于长度,即使它是最大的二位数,我是最小的三位数,我依然大于它,因此可以使用BFS,使用它去判断从这一点所能到达的最大长度,如果这个长度小于我之前所保留的最大长度,那么就不用再搜了,直接跳过。
还有一种情况,就是BFS出来的数长度和之前所保留的最大数长度相等呢?既然已经使用BFS做搜索预判,那么就不如在记录好从那一点所到达的最长距离所形成的数记录下来。然后比较这个数和保留的最大数,如果它小,那就甭走这走一步了
#include"iostream"
#include"cstring"
#include"queue"
#include"ctype.h"
#include"algorithm"
using namespace std;
char a[33][33];
int can[33];
int book[33][33];
int book2[33][33];
int m,n;
int nex[4][2]={{0,1},{1,0},{-1,0},{0,-1}};
int tx,ty;
bool cmp(int a,int b)
{
return a>b;
}
typedef struct Node
{
int no[33], len;
void Init() {
len = 0;
}
bool operator < (const Node &rhs) const {
if(len != rhs.len) return len < rhs.len;
for(int i = 0; i < len; ++i)
if(no[i] != rhs.no[i]) return no[i] < rhs.no[i];
return false;
}
}Node;
Node ans,now;
int bfs(int x,int y)
{
queue<int> que; que.push(x *33 + y);
int f = 1;
can[0] = a[x][y] - ‘0‘;
memset(book2, 0, sizeof(book2));
book2[x][y] = 1;
while(!que.empty()) {
int tmp = que.front(); que.pop();
int nx = tmp /33, ny = tmp % 33;
for(int i = 0; i < 4; ++i) {
int px = nx + nex[i][0], py = ny + nex