标签:
啊~第三天了,前两天的总结还没写完……
今天接着昨天的斜率优化继续,具体介绍了叉积和下凸壳。
叉积是什么呢?叉积可是一个神奇的东西。
叉积也称为向量的外积,与内积不同,两个向量的外积依旧是一个向量,并且与这两个向量垂直。
那么叉积有什么用呢?跟斜率优化有什么关系呢?
•在平面几何中,可以用来判断两个向量的顺时针逆时针关系。
设A = [x1, y1] ,B = [x2, y2]
若x1 * y2 – x2 * y1 > 0,则B在A的逆时针方向,x1 * y2 – x2 * y1 < 0,则B在A的顺时针方向,x1 * y2 – x2 * y1 = 0,A与B平行。
有了叉积我们就可以判断一个新加入的节点是在当前最右节点的右上方还是右下方。
如图一:在图一的情况中,我们直接将新节点加入到凸壳中。
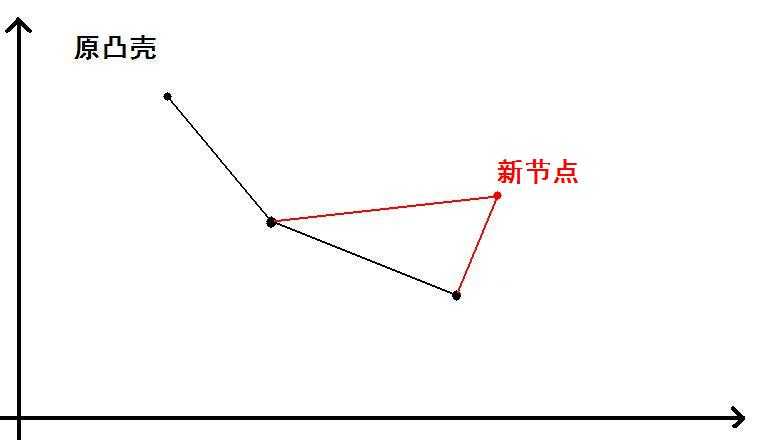
而图二中,我们应当删除最后一个元素。在每次删除之后,我们都还应继续比较删除后的最后一个节点。直到出现图一的情况。
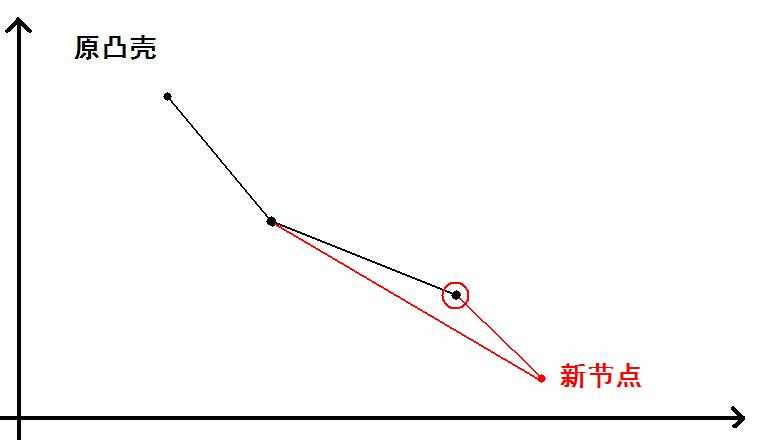
这里以一个例题的代码作为模板学习:

1 struct Vector 2 { 3 LL x, y; 4 Vector() {} 5 Vector(LL _x, LL _y) 6 { 7 x = _x; y = _y; 8 } 9 Vector operator -(const Vector &a) const 10 { 11 return Vector(x - a.x, y - a.y); 12 } 13 } que[N]; 14 15 LL cross(Vector a, Vector b)//叉积判断新节点与末节点的位置关系 16 { 17 return a.x * b.y - a.y * b.x; 18 } 19 20 int head, tail; 21 void add(Vector p) 22 { 23 while(tail - head >= 2)//队列中存在至少两个节点 24 { 25 if(cross(que[tail - 1] - p, que[tail - 2] - p) < 0) break; 26 --tail; 27 } 28 que[tail++] = p; 29 }
而对于查询,我们每次找到相同斜率下,截距最小的点作为结果返回。

1 LL cal(Vector p, LL k) //计算需要求出的值 2 { 3 return p.y - k * p.x; 4 } 5 6 LL read(LL k) 7 { 8 while(head + 1 < tail) 9 { 10 if(cal(que[head], k) < cal(que[head + 1], k)) break;//找到第一个权值大于当前点的位置,根据单调性,所有更靠右的点的权值都大于当前改点 11 ++head; 12 } 13 return cal(que[head], k); 14 }
(……正在施工……)
标签:
原文地址:http://www.cnblogs.com/hy-dgj/p/4696670.html