标签:
题目地址:http://poj.org/problem?id=1419
| Time Limit: 1000MS | Memory Limit: 10000K | |||
| Total Submissions: 4468 | Accepted: 2042 | Special Judge | ||
Description
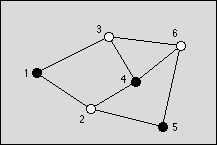
Input
Output
Sample Input
1 6 8 1 2 1 3 2 4 2 5 3 4 3 6 4 6 5 6
Sample Output
3 1 4 5
题目解读:对于一个给定的图找出一个最佳的着色。对图中的节点进行着色,只能用黑色或白色,着色的规则就是两个相邻的节点不能都是黑色。
(当然有可能是白色)T组数据,每组有n个节点,m条边。也就是要求当前图的最大独立集。
算法实现:通过求补图上的最大团来计算当前图的最大独立集。补图直接在输入边的时候就构建,采用规定模式计算补图最大团。
代码:

1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <ctype.h> 5 #include <math.h> 6 #include <iostream> 7 #include <string> 8 #include <queue> 9 #include <algorithm> 10 #define N 105 11 12 using namespace std; 13 14 int n, m; 15 bool g[N][N]; 16 int get[N][N]; 17 int node[N], ans[N], dp[N]; 18 19 int Max; //当前团的节点数为Max 20 21 22 void dfs(int now, int sum) 23 { //从当前状态(当前团的节点数为now 与其中最后节点相连的边数为sum)出发,递归计算最大团 24 if(sum==0){ //若构成团 即完全子图 25 if(now > Max){ 26 Max=now; 27 for(int i=1; i<=Max; i++) 28 ans[i]=node[i]; //存储团中的节点 29 } 30 return ; 31 } 32 for(int i=1; i<=sum; i++){ 33 int v=get[now][i], t=0; 34 if(now+dp[v]<=Max) return ; 35 for(int j=i+1; j<=sum; j++){ 36 if(g[v][get[now][j]] ) 37 get[now+1][++t]=get[now][j]; 38 } 39 node[now+1]=v; 40 dfs(now+1, t); 41 } 42 } 43 44 void init() 45 { 46 scanf("%d %d", &n, &m); 47 memset(g, true, sizeof(g)); //补图初始化 边之间互相连通 48 for(int i=0; i<m; i++){ 49 int u, v; 50 scanf("%d %d", &u, &v); 51 g[u][v]=false; g[v][u]=false; //补图中应该断开 52 } 53 } 54 55 void solve() //计算和输出补图的最大团 即是原图的最大独立集 56 { 57 Max=0; // 58 for(int i=n; i>=1; i--){ //按照递减顺序将每个节点i作为当前团的首节点 59 int sum=0; 60 for(int j=i+1; j<=n; j++){ //计算i+1...n中与i相邻的端点,将其存入get[1][] 61 if(g[i][j]) get[1][++sum]=j; 62 } 63 node[1]=i; 64 dfs(1, sum); 65 dp[i]=Max; 66 } 67 printf("%d\n", Max); 68 for(int i=1; i<=Max-1; i++){ 69 printf("%d ", ans[i]); 70 } 71 printf("%d\n", ans[Max]); 72 } 73 74 int main(void) 75 { 76 int tg; 77 scanf("%d", &tg); 78 while(tg--){ 79 init(); 80 solve(); 81 } 82 return 0; 83 }
poj 1419Graph Coloring 【dfs+补图+计算最大团+计算最大独立集 【模板】】
标签:
原文地址:http://www.cnblogs.com/yspworld/p/4701037.html