标签：
从学导数那天开始，就差不多接触到了牛顿法求解零点的精髓，那时局限于一维，且只是从几何上认识到它。
一、主要作用
（1）求零点
（2）优化（求最大最小值）
二、求零点
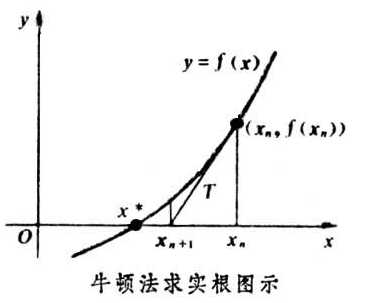求f(x)=0.
解：如图，满足近似关系
斜率k=f‘(xn)
xn+1≈xn-f(xn)/k
解得：
xn+1≈xn-f(xn)/f‘(xn) ...(1)
三、优化
而对于优化问题，不过是求maxf(x).
解：题目等价于f‘(x)=0.
根据(1)式，有
xn+1≈xn-f’(xn)/f‘‘(xn) ...(2)
四、另外的证明（对于向量）
（1）求零点
展开成一阶泰勒，有
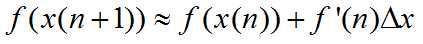
令
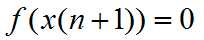
于是
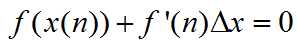
又
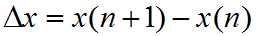
得到
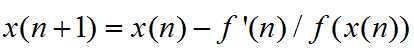
（2）优化（求最大最小值）
根据二阶泰勒公式
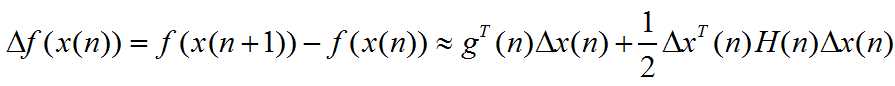
对Δx求导，得
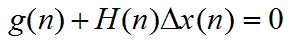
解得
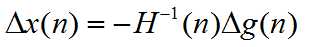
于是，有
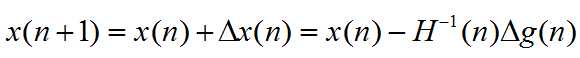
这里，g(n)是f(n)的一阶导数，H(n)是f(n)的二阶导数。
参考文献
（1）http://blog.csdn.net/luoleicn/article/details/6527049
（2）《神经网络与机器学习》
标签：
原文地址：http://www.cnblogs.com/Wanggcong/p/4702692.html
