标签:
Description
Input
Output
| input | output |
|---|---|
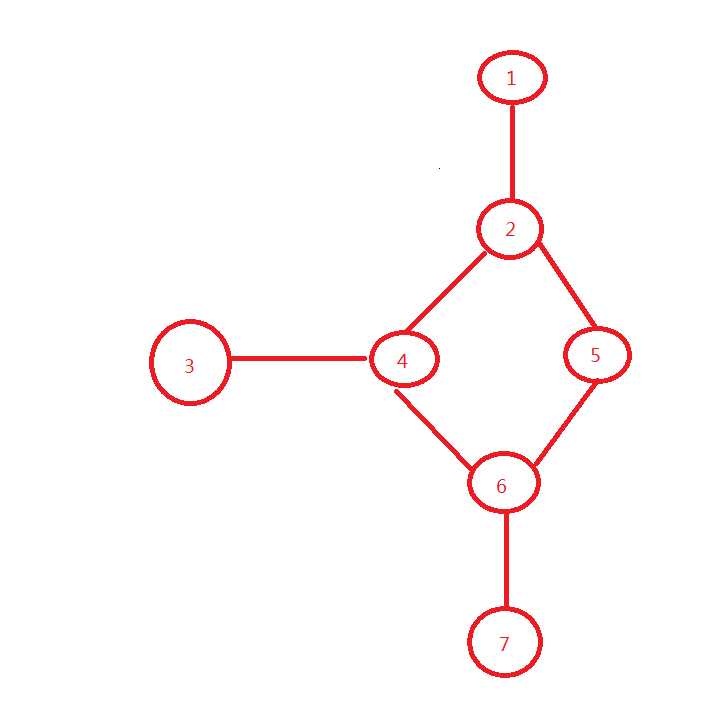
7 7 1 2 2 4 2 5 3 4 4 6 5 6 6 7 1 7 3 |
2 |
#include <cstdio> #include <vector> #include <queue> #include <cstring> using namespace std; const int maxn = 1e5 + 50; #define max(x,y) ((x)>(y)?(x):(y)) #define min(x,y) ((x)<(y)?(x):(y)) vector<int>e[maxn]; int dp[maxn] , d[maxn] , maxv[maxn], n , m , s , f , r , used[maxn] ; queue<int>q; void solve() { memset(dp , 0 , sizeof(dp));memset(d,-1,sizeof(d));memset(maxv,-1,sizeof(maxv));memset(used,0,sizeof(used)); d[f] = 0; q.push(f); while(!q.empty()) { int x = q.front();q.pop(); for(int i = 0 ; i < e[x].size() ; ++ i) { int v = e[x][i]; if (d[v] == -1) { d[v] = d[x] + 1; q.push(v); } } } maxv[r] = 0; q.push(r); while(!q.empty()) { int x = q.front();q.pop(); for(int i = 0 ; i < e[x].size() ; ++ i) { int v = e[x][i]; if (maxv[v] == -1) { maxv[v] = maxv[x] + 1; q.push(v); } } } dp[s] = maxv[s];used[s] = 1; q.push(s); while(!q.empty()) { int x = q.front();q.pop(); maxv[x] = min(maxv[x],dp[x]); for(int i = 0 ; i < e[x].size() ; ++ i) { int v = e[x][i]; if (d[x] - d[v] == 1) { dp[v] = max(dp[v],maxv[x]); if (!used[v]) { q.push(v); used[v] = 1; } } } } printf("%d\n",maxv[f]); } int main(int argc,char *argv[]) { scanf("%d%d",&n,&m); while(m--) { int u ,v ; scanf("%d%d",&u,&v);u--,v--; e[u].push_back(v);e[v].push_back(u); } scanf("%d%d%d",&s,&f,&r);s--,f--,r--; solve(); return 0; }
标签:
原文地址:http://www.cnblogs.com/Xiper/p/4703597.html