标签:
栈
栈(stack)是限定尽在表尾进行插入或删除操作的线性表。与线性表类似,栈也有两种存储表示方式。
下面是顺序栈的实现。

1 #include <stdio.h> 2 #include <malloc.h> 3 #define MaxSize 100 4 typedef char ElemType; 5 //定义顺序栈 6 typedef struct 7 { 8 ElemType data[MaxSize]; 9 //栈顶指针 10 int top; 11 }SqStack; 12 13 //初始化栈 14 void InitStack(SqStack *&s) 15 { 16 s=(SqStack *)malloc(sizeof(SqStack)); 17 s->top=-1; 18 } 19 20 //销毁栈 21 void DestroyStack(SqStack *s) 22 { 23 free(s); 24 } 25 26 //判断栈空 27 bool StackEmpty(SqStack *s) 28 { 29 return (s->top==-1); 30 } 31 32 //进栈 33 bool Push(SqStack *&s,ElemType e) 34 { 35 //栈满的时候 36 if(s->top==MaxSize-1) 37 return false; 38 s->data[++s->top]=e; 39 return true; 40 } 41 42 //出栈 43 bool Pop(SqStack *&s,ElemType &e) 44 { 45 //栈空的时候 46 if(s->top==-1) 47 return false; 48 e=s->data[s->top--]; 49 return true; 50 } 51 52 //取栈顶元素 53 bool GetTop(SqStack *&s,ElemType &e) 54 { 55 //栈空的时候 56 if(s->top==-1) 57 return false; 58 e=s->data[s->top]; 59 return true; 60 }
使用栈我们可以有很多应用。
下面将演示使用栈进行数制转换。
十进制数N和其他d进制数的转换时计算机实现计算的基本问题,下面的简单算法基于下列原理:
N=(N div d)×d+N mod d(其中:div为整除运算,mod为求余运算)
下面是该算法的实现

1 void conversion() 2 { 3 //构造空栈 4 SqStack *s; 5 InitStack(s); 6 //获取任意一个非负十进制整数 7 unsigned int n; 8 scanf("%d",&n); 9 //算法核心 10 while(n) 11 { 12 Push(s,n%8); 13 n=n/8; 14 } 15 while(!StackEmpty(s)) 16 { 17 ElemType e; 18 Pop(s,e); 19 printf("%d",e); 20 } 21 }
下面将演示使用栈求解迷宫问题
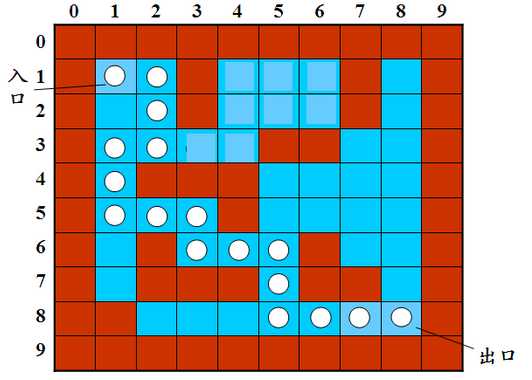
计算机求解迷宫问题的时候通常用的是“穷举求解”的方法,即从入口出发,顺着某一方向向前搜索,若能走通,则继续往前走;否则沿原路退回,换一个方向在继续搜索,直到所有可能的通路都搜索到为止。
显然,我们需要用到一个后进先出的数据结构来保存从入口到当前为止的路径,所有应用“栈”来解决是自然而然的事情。
算法的基本思想:
若当前位置”可通“,则纳入”当前路径“,并继续朝”下一个位置“搜索,如此重复直到到达出口。
若当前为止”不可通“,则应退回“前一通道块”,然后朝着其他方向继续探索,若该通道块的四周均“不可通”,则应从“当前路径”上删除该通道块。
下面是算法的实现。(利用一个二维数组代表迷宫,1代表墙,0代表通道)

1 #include <stdio.h> 2 #define M 4 //行数 3 #define N 4 //列数 4 #define MaxSize 100 5 //maze表示一个迷宫,在其四周加上均为1的墙 6 int maze[M+2][N+2]= 7 { 8 {1,1,1,1,1,1},{1,0,0,0,1,1},{1,0,1,0,0,1}, 9 {1,0,0,0,1,1},{1,1,0,0,0,1},{1,1,1,1,1,1} 10 }; 11 12 //定义栈和存放最短路径的数组 13 struct 14 { 15 int x,y; //横纵坐标 16 int di; //用来表示该通道块上下左右是否可通 初始化为-1 17 }Stack[MaxSize],Path[MaxSize]; 18 int top=-1; //栈顶指针 19 int count=1; //路径长度计数 20 int minlen=MaxSize; //最短路径长度 21 22 //迷宫求解 参数为迷宫入口跟出口的位置 23 void GetPath(int xi,int yi,int xe,int ye) 24 { 25 int i,j,di,find,k; 26 top++; 27 //入口通道块进栈 28 Stack[top].x=xi; 29 Stack[top].y=yi; 30 Stack[top].di=-1; 31 maze[xi][yi]=-1; 32 //栈不为空时循环 33 while(top>-1) 34 { 35 i=Stack[top].x; 36 j=Stack[top].y; 37 di=Stack[top].di; 38 //找到了出口 39 if(i==xe&&j==ye) 40 { 41 //更新最短路径 42 if(top+1<minlen) 43 { 44 for(k=0;k<=top;k++) 45 Path[k]=Stack[k]; 46 minlen=top+1; 47 } 48 //让该位置标为其他路径可走节点 49 maze[Stack[top].x][Stack[top].y]=0; 50 top--; 51 i=Stack[top].x; 52 i=Stack[top].y; 53 di=Stack[top].di; 54 } 55 find=0; 56 //找下一个可走方块 57 while(di<4&&find==0) 58 { 59 di++; 60 //遍历4个方向 61 switch(di) 62 { 63 case 0:i=Stack[top].x-1;j=Stack[top].y;break; 64 case 1:i=Stack[top].x;j=Stack[top].y+1;break; 65 case 2:i=Stack[top].x+1;j=Stack[top].y;break; 66 case 3:i=Stack[top].x;j=Stack[top].y-1;break; 67 } 68 if(maze[i][j]==0) find=1; 69 } 70 //找到了下一个可走方块 71 if(find==1) 72 { 73 Stack[top].di=di; 74 top++; 75 Stack[top].x=i; 76 Stack[top].y=j; 77 Stack[top].di=-1; 78 //避免重复走到该方块 79 maze[i][j]=-1; 80 } 81 //没有路可走,则退回 82 else 83 { 84 //让该位置标为其他路径的可走节点 85 maze[Stack[top].x][Stack[top].y]=0; 86 top--; 87 } 88 } 89 //输出最短路径 90 printf("其中一条最短路径如下:\n"); 91 for(k=0;k<minlen;k++) 92 { 93 printf("(%d %d) ",Path[k].x,Path[k].y); 94 } 95 printf("\n"); 96 }
标签:
原文地址:http://www.cnblogs.com/runnyu/p/4704773.html