标签:
GBDT之前实习的时候就听说应用很广,现在终于有机会系统的了解一下。
首先对比上节课讲的Random Forest模型,引出AdaBoost-DTree(D)

AdaBoost-DTree可以类比AdaBoost-Stump模型,就可以直观理解了
1)每轮都给调整sample的权重
2)获得gt(D,ut)
3)计算gt的投票力度alphat
最后返回一系列gt的线性组合。
weighted error这个比较难搞,有没有不用动原来的模型,通过输入数据上做文章就可以达到同样的目的呢?
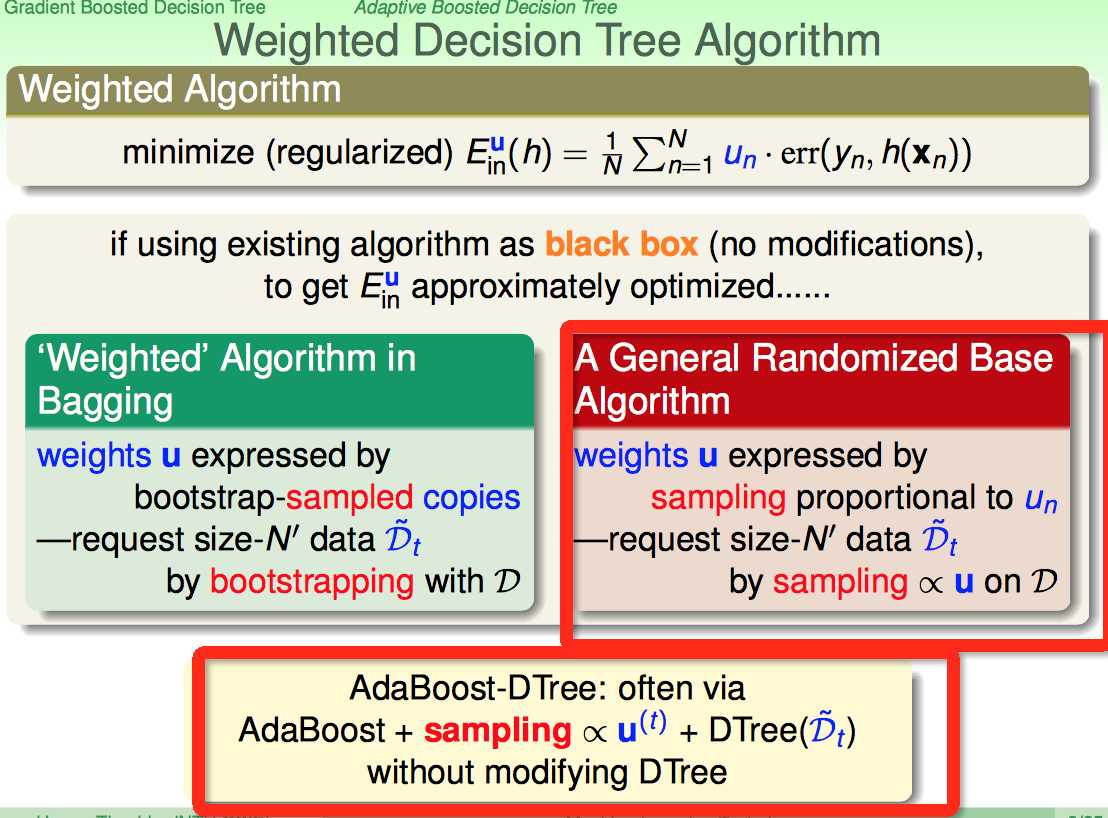
回想bagging的weighted策略:每轮boostrapping的时候,样本的权重体现在copy个数上。
现在从一个更一般的角度来看,给定一个weighted u,如果对数据按照u的比例大小对样本进行sampling的动作,那么最后D中的数据也体现了weighted。
这样AdaBoost-DTree的原型就出来了:
1)AdaBoost方法
2)按照给定的权重对样本进行sampling的动作,生成每棵树的训练数据
3)训练每棵树
这种方法如果不限制树的高度,是容易产生autocracy的。原因是如果把所有的资料丢进去,容易全切开。
这里产生一个疑问:为什么random forest中每棵树就不会有这种完全切开全分开的情况,甚至在decision stump那个作业的时候,会不会有某个stump给全切开了。
1)个人感觉random forest样本、特征、分支条件(b(x))都是randomness的,完全分开的可能性极小极小
2)至于decision stump,如果真有个decision stump能一刀切开,那也就不用这么复杂的模型了

总的来说,每棵树要弱一些。
如果弱到不能再弱,树就只留下一层了,这时候decision tree就退化成了decision stump了。

接下来,林开始讲解AdaBoost方法的一些optimization view以及内在的insights,这里的一些推导大体思路记住就可以了。
AdaBoost的核心是每个样本的权重变化,所谓的insights也是从这里出发。

1)把之前讲授的AdaBoost样本权重迭代公式转换一下形式(重点是引入了alphat):
unt+1 = unt * exp(-yn * alphat * gt(xn))
2)根据修改后的迭代公式,给出了每个样本在T+1轮的权重通项公式:
unT+1 = 1/N * exp(- yn * Σt=1,T (alphat * gt(xn)) )
(这里有个地方在之前提到过,一般N个样本,每个样本的初始权重系那个灯,都是1/N)
综合上面两点,unT+1 与 前面T轮产生的所有gt对样本点xn的综合打分情况(Σt=1,T (alphat * gt(xn))) 有关系。

林在这里点出了一个insights:可以把voting score和margin联系起来,类比SVM中的margin概念。
1)把每个gt(xn)看成是xn的一种transform,前面的alphat看成是transformed之后的权重
2)这种形式很像hard-margin SVM中的margin
我们肯定是希望yn*(voting score)越大越好,因为这代表预测值跟实际值更靠近;因此我们可以得到unT+1有可能随着T增加而变小。
顺着这种思路,AdaBoost的大方向最起码应该是unT+1越小越好,那么Σn=1,N(unt)也应该是随着AdaBoost的迭代而逐步减小的。
因此,思路就是:预测的准 → yn*(voting score)越大越好 → ΣunT+1越小越好
于是,AdaBoost的优化目标函数就可以大概给出来了。

再次请出来我们的老朋友error0/1,对比一下AdaBoost又产生了一个bound住error0/1的上界的error measure,叫“exponential error measure”
如下图:

既然目标函数大概写出来了,下面就是怎么最小化这个目标函数了。
这个任务比较麻烦,因为是Σ套着exp再套着Σ,因此需要一些前人的智慧了。
模仿gradient descent的方法,假设前面已经AdaBoost完t-1轮了,现在要求的是一个函数gt(x)(或者称为h(x))。
再第t轮,我们沿着函数h(x)的方向走ita的步长,可以使得目标函数迅速往min的方向走。如下:

1)由于前面已经执行完了t-1轮,因此可以把式子化简一下,把一些项目合并成unt的函数形式
2)利用xn=0点的泰勒展开,进一步化简(这里为什么要用0这个位置的taylor展开呢,可以理解成h(x)只是沿着原来的Σ1,t-1(alphat*g‘(xn)这个函数,挪动的了一小步;这一小步,就意味着变化很小,变化很小甚至接近0,因此就可以在0点taylor展开。不晓得这种理解是否正确,意会吧)
到此,我们利用前人的智慧已经把目标函数给大大简化了,要求的东西有俩:
1)h(x)是啥?
2)ita是啥?

这里的方法还是挺巧妙的
1)先提出来一个固定的Σunt,后面留出来的“变化的一项”
2)再分析下后面变化的这一项,如果要后面变化这一项最小,那么就是最小化Einu(h)(周边再配合上一些常系数)
因此,可以获得结论:在AdaBoost的过程中,算法A就是good gt了!
下面再看ita如何求。

核心在于EADA是怎么变成可对ita求导的形式的:
EADA = u1t*exp(-ita) + u2t*exp(ita)...
EADA1 = u1t*exp(-ita) + ut2t*0 ... (EADA1只考虑exp(-ita)的项,其余的补上0)
EADA2 = u1t*0 + u2t * exp(ita) ...(EADA2只考虑exp(+ita)的项,其余的补上0)
则,EADA = EADA1 + EADA1 = (Σunt) * ( (1-epson)exp(-ita) + epson*exp(ita) )
随后的求导步骤就是很自然的了,因此就验证了之前的结论,itat = sqrt( (1-epsont)/epsont) )就是最优的。前一次课直接给出了这个结论,并没有说为什么,这次算是给出了一个相对理论些的推导。
再往更一般的Gradient Boost推广。
推广的方式就是泛化error measure function,如下:

沿着这个思路,下面往regression的方向上平移一下。
大体的目标还是两个:
1)求解函数h(x)的形式
2)求解函数h(x)移动的幅度
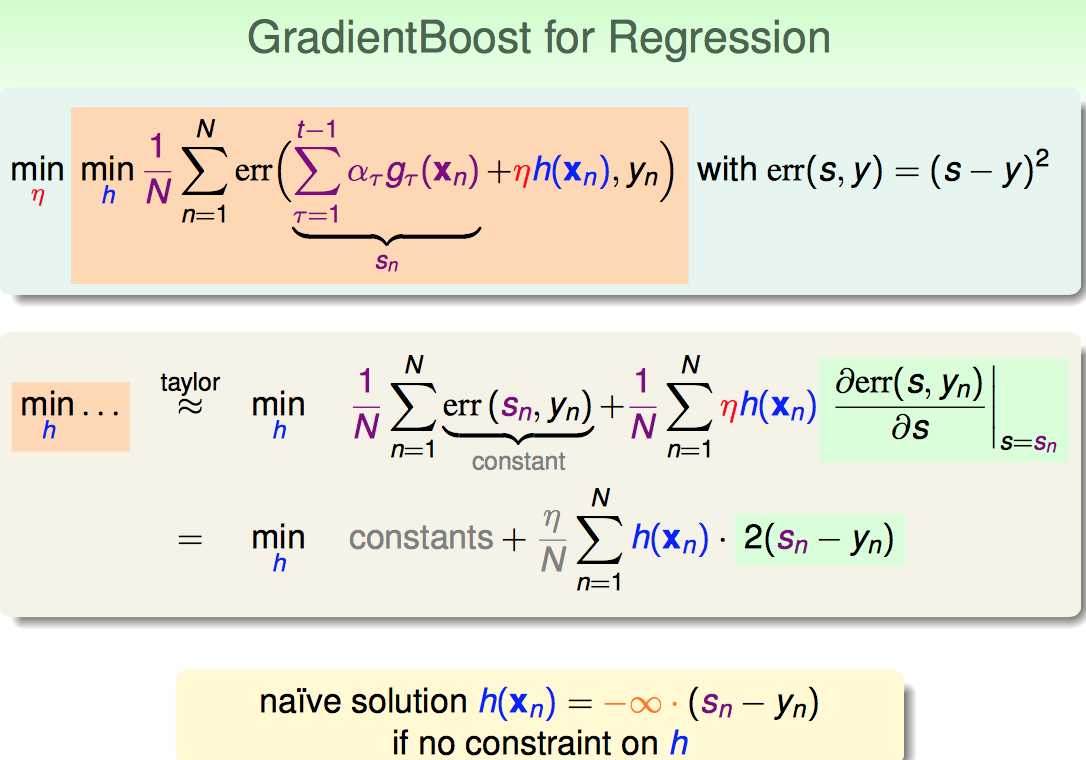
先搞定h(x)的形式
regression一般用square error,直接上taylor:
1)前面一项是constant,因为yn都知道sn也都知道
2)第二项要对s求导 并在sn这点取导数值
这样,看起来貌似h(x)无穷大;这样不科学,于是要添加对于h(x)的惩罚项。

再经过penalize一番折腾之后,h终于有个像模像样的形式了:即regression with residuals。
接下来再解决移动幅度的问题。

一番云雨之后,alphat也求出来了,就是一个单变量的线性回归。
把前面的铺垫都做好了之后,简练地给出了GBDT的形式:

1)利用C&RT去学{x, yn-sn},保留这一轮学出来的树gt(x)
2)再求{gt(x), residual}线性回归,最小化目标函数求出来ita
3)更新sn
学习足够多次数后,返回组合的GBDT。
【Gradient Boosted Decision Tree】林轩田机器学习技术
标签:
原文地址:http://www.cnblogs.com/xbf9xbf/p/4706150.html