poj 2513 Colored Sticks(欧拉回路 并查集 路径压缩 字典树)(困难)

标签：

Description

Input

Output

Sample Input

blue red
red violet
cyan blue
blue magenta
magenta cyan

Sample Output

Possible

题意：

给定一些木棒，木棒两端都涂上颜色，求是否能将木棒首尾相接，连成一条直线，要求不同木棒相接的一边必须是相同颜色的。

思路：

这题不错，用到了三个知识点，我开始没用字典树，超时了。顺便学习了字典树。

看到了一个不错的题解。

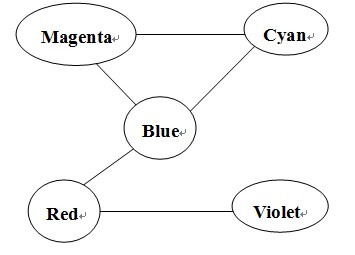
可以用图论中欧拉路的知识来解这道题，首先可以把木棒两端看成节点，把木棒看成边，这样相同的颜色就是同一个节点

问题便转化为：

给定一个图，是否存在“一笔画”经过涂中每一点，以及经过每一边一次。

这样就是求图中是否存在欧拉路Euler-Path。

回顾经典的“七桥问题”，相信很多同学马上就明白了什么是 欧拉路 了，这里不多作解释。

由图论知识可以知道，无向图存在欧拉路的充要条件为：

①     图是连通的；

②     所有节点的度为偶数，或者有且只有两个度为奇数的节点。

其中①图的连通性用程序判断比较麻烦，先放一下。

这里先说说②关于度数的判断方法：

Blue=3

Red=2

Violet=1

Cyan=2

Magenta=2

用一个一维数组就能记录了，然后分别 模2，就能判断颜色结点的奇偶性

只要奇度数的结点数的个数 = 1 或 >=3 ，即使①图连通，欧拉路也必不存在

但是若 奇度数的结点数的个数 为0或 ==2，那么我们继续进行①图的连通性证明：

证明①图的连通性，使用并查集MergeSet是非常高效的方法。

基本方法：

初始化所输入的n个结点为n棵树，那么就有一个n棵树的森林，此时每棵树的有唯一的结点（根），该结点的祖先就是它本身。再通过不断地输入边，得到某两个结点（集合）之间的关系，进而合并这两个结点（集合），那么这两个集合就构成一个新的集合，集合内的所有结点都有一个共同的新祖先，就是这个集合（树）的根。

最后只要枚举任意一个结点，他们都具有相同的祖先，那么就能证明图时连通的了。

但是单纯使用并查集是会超时的，因为这样会导致每次寻找某个结点的祖先时，平均都会花费O(n/2)时间，最坏情况，当n==50W时，O(n/2)大概为25ms，那么要确定50W个结点是否有共同祖先时，总费时为50W*25ms ，铁定超，不算了= =

因此必须使用并查集时必须压缩路径，前几次搜索某个结点k的祖先时，在不断通过父亲结点寻找祖先结点时，顺便把从k到最终祖先结点S中经过的所有结点的祖先都指向S，那么以后的搜索就能把时间降低到O(1)

由于并查集必须利用 数组的下标 与 存储的对象，使用int是比较方便的处理方法，但是题目的“颜色结点”是string，不方便用来使用并查集，即使用map也不行，虽然STL的map是基于hash的基础上，但并不高效，在本题中使用会超时。

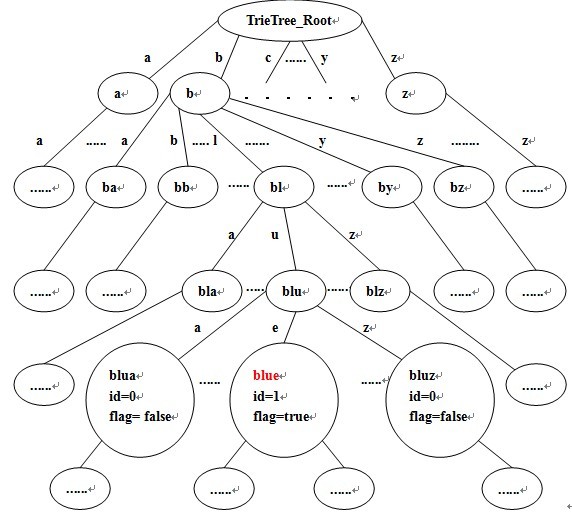
为此可以使用Trie字典树，得到每个颜色单词对应的int编号id ，可以说利用Trie把string一一映射到int，是本题后续处理的关键所在。关于动态创建字典树的方法去百度，这里不多说，下面只用用一个图简单说明一下用Trie字典树标识第一个颜色单词blue：

这个题目涉及了多个基本数据结构和算法，综合性很强，非常有代表性，能够A到这题确实是受益良多。

知识考查点：

1、字典树；

2、欧拉路：其中又考察了判断是否为连通图；

3、并查集 及其优化方法（路径压缩）。

输出：

POSSIBLE：  奇度数结点个数==0 或 ==2  且  图连通

IMPOSSIBLE：奇度数结点个数==1 或 >=3  或  图不连通

PS:注意创建TrieTree链表时，C++不存在NULL，要用 0 替代 NULL

代码：

//超时的

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
#define maxx 250000
struct edge
{
    int u,v;
}e[maxx];
char color1[15],color2[15];
int in[maxx],out[maxx],bused[maxx];
char col[maxx][12];
int pre[maxx];
int num,sum;

int turn(char *s)
{
    int i;
    for(i=0;i<sum;i++)
    {
        if(strcmp(col[i],s)==0)
            return i;
    }
    if(i==sum)
    {
        strcpy(col[sum],s);
        sum++;
        return sum-1;
    }
}

int Find(int x)
{
    int s;
    for(s=x;pre[s]>=0;s=pre[s]);
    while(s!=x)
    {
        int tmp=pre[x];
        pre[x]=s;
        x=tmp;
    }
    return s;
}


void Union(int R1,int R2)
{
    int r1=Find(R1),r2=Find(R2);
    int tmp=pre[r1]+pre[r2];
    if(pre[r1]>pre[r2])
    {
        pre[r1]=r2;
        pre[r2]=tmp;
    }
    else
    {
        pre[r2]=r1;
        pre[r1]=tmp;
    }
}

int connect()
{
    int u,v;
    for(int i=0;i<sum;i++)
        pre[i]=-1;
    for(int i=0;i<num;i++)
    {
        u=e[i].u,v=e[i].v;
        if(u!=v && Find(u)!=Find(v))
            Union(u,v);
    }
    int first=-1,i;
    for(i=0;i<sum;i++)
    {
        if(!bused[i]) continue;
        if(first==-1) first=i;
        else if(Find(i)!=Find(first)) break;
    }
    if(i<sum)
        return 0;
    else
        return 1;
}

int main()
{
    memset(in,0,sizeof(in));
    memset(out,0,sizeof(out));
    memset(bused,0,sizeof(bused));
    num=0;sum=0;
    scanf("%s%s",color1,color2);
    strcpy(col[0],color1);
    strcpy(col[1],color2);
    sum=2;
    e[0].u=0,e[0].v=1;
    out[0]++;in[1]++;
    bused[0]=bused[1]=1;
    num=1;
    int qq=1;
    while(scanf("%s%s",color1,color2)!=EOF)
    {
        int u=turn(color1),v=turn(color2);
        e[num].u=u,e[num].v=v;
        out[u]++;in[v]++;
        bused[u]=bused[v]=1;
        num++;qq++;
        if(qq==5)
            break;
    }

    for(int i=0;i<num;i++)
        cout<<e[i].u<<" "<<e[i].v<<endl;

    for(int i=0;i<sum;i++)
        cout<<i<<" in:"<<in[i]<<"  out:"<<out[i]<<endl;

    cout<<"点："<<sum<<" "<<"边："<<num<<endl;
    int flag=1;
    int one=0,none=0;
    for(int i=0;i<sum;i++)
    {
        if(!bused[i])continue;
        if(out[i]-in[i]>=2||in[i]-out[i]>=2){flag=0;break;}
        if(out[i]==0&&in[i]==0){flag=0;break;}
        if(out[i]-in[i]==1)
        {
            one++;
            if(one>1){flag=0;break;}
        }
        if(in[i]-out[i]==1)
        {
            none++;
            if(none>1){flag=0;break;}
        }

    }
    if(one!=none) flag=0;
    if(!connect()) flag=0;
    if(flag)
        printf("Possible\n");
    else
        printf("Impossible\n");
    return 0;
}

#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
//79372K 1157MS
//trie+并查集+欧拉路径
const int maxnum=500010;
int degree[maxnum],parent[maxnum],rank[maxnum];
int n=1;
struct node
{
    int id;
    bool use;
    node *next[27];
    node()
    {
        id=0;
        use=false;
        int i;
        for(i=0;i<27;i++)
            next[i]=NULL;
    }
};
node *root;

int hash(char *str)
{
    node *p=root;
    int k;
    while(*str!=0)
    {
        k=*str-'a';
        if(p->next[k]==NULL)
            p->next[k]=new node();
        p=p->next[k];
        str++;
    }
    if(!p->use)
    {
        p->id=n;
        n++;
        p->use=true;
        return p->id;
    }
    else
        return p->id;
}

int find(int u)
{
    if(u!=parent[u])
        parent[u]=find(parent[u]);
    return parent[u];
}

void Union(int i,int j)
{
    if(rank[i]<rank[j])
        parent[i]=j;
    else
    {
        parent[j]=i;
        if(rank[i]==rank[j])
            i++;
    }
}

int main()
{
    char a[15],b[15];
    int i;
    root=new node();
    for(i=1;i<maxnum;i++)
        parent[i]=i;
    while(scanf("%s%s",a,b)!=EOF)
    {
        int k=hash(a);
        int l=hash(b);
        degree[k]++;
        degree[l]++;

        int p=find(k);
        int q=find(l);
        if(p!=q)
            Union(p,q);
    }
    int t=find(1);
    int num=0;  //度数为奇数的结点个数
    for(i=1;i<n;i++)
    {
        if(find(i)!=t)//存在多个祖先，图为森林，不连通
        {
            printf("Impossible\n");
            return 0;
        }
        if(degree[i]%2==1)
            num++;
        if(num>2)  //度数为奇数的结点数大于3，欧拉路必不存在
        {
            printf("Impossible\n");
            return 0;
        }
    }
    if(num==1)  //度数为奇数的结点数等于1，欧拉路必不存在
        printf("Impossible\n");
    else   //度数为奇数的结点数恰好等于2或不存在，存在欧拉路
        printf("Possible\n");
    return 0;
}

poj 2513 Colored Sticks(欧拉回路 并查集 路径压缩 字典树)(困难)

标签：

原文地址：http://blog.csdn.net/kaisa158/article/details/47322917