标签:
游客请绕路:
http://www.cnblogs.com/xin-hua/p/3242428.html
http://blog.csdn.net/u013368721/article/details/45827909
结论:
1、不加限制答案:f[n]=∑(-1)^(k-1)*(f[n-k*(3*k-1)/2]+f[n-k*(3*k+1)/2])
其中n-k*(3*k-1)/2>=0,n-k*(3*k+1)/2>=0 注意两个条件要分开判断,有大于0的就加上相应的f。
2、
 表示成刚好
表示成刚好 个正整数之和时,可以表示为
个正整数之和时,可以表示为 。显然,
。显然, 。
。 对于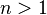 ,
,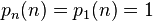

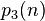 = 最接近
= 最接近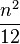 的正整数。
的正整数。

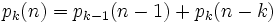
3、
令Fk(n)表示n的满足数拆分时每种数的个数小于等于k的数拆分方案数。则有:
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; long long f[100010] ; //:f[n]=∑(-1)^(k-1)*(f[n-k*(3*k-1)/2]+f[n-k*(3*k+1)/2]) /* 其中n-k*(3*k-1)/2>=0,n-k*(3*k+1)/2>=0; 注意两个条件要分开判断,有大于0的就加上相应的f,不是两个同时成立或者不成立 const int mod = 1000000007; */ const int mod=1000000007; void dabiao() { memset(f,0,sizeof f) ; f[0]= 1,f[1]=1 ,f[2] = 2 ; int flag= -1; for(int i=3 ; i<=100005;i++){ for(int j=1 ; ;j++){ if(j % 2) flag =1; else flag=-1; int t = (i - j*(3*j-1)/2) ; int ct = (i-j*(3*j+1)/2); if(t < 0&& ct<0 ) break; if(t>=0){ f[i]=(f[i] + flag*f[t]) % mod; } if(ct>=0){ f[i]=(f[i]+flag*f[ct]) % mod ; } } f[i] = (f[i] + mod)% mod ; } } int main() { dabiao() ; int t; scanf("%d",&t) ; while(t--){ int n; scanf("%d",&n); cout<<f[n]<<endl; } return 0; }
hdu 4658 限制每个数字出现的次数不能超过 m
#include <iostream> #include <cstdio> #include <cstring> #include <algorithm> using namespace std; long long f[100010] ; //:f[n]=∑(-1)^(k-1)*(f[n-k*(3*k-1)/2]+f[n-k*(3*k+1)/2]) /* 其中n-k*(3*k-1)/2>=0,n-k*(3*k+1)/2>=0; 注意两个条件要分开判断,有大于0的就加上相应的f,不是两个同时成立或者不成立 const int mod = 1000000007; */ const int mod=1000000007; void dabiao() { memset(f,0,sizeof f) ; f[0]= 1,f[1]=1 ,f[2] = 2 ; int flag= -1; for(int i=3 ; i<=100005;i++){ for(int j=1 ; ;j++){ if(j % 2) flag =1; else flag=-1; int t = (i - j*(3*j-1)/2) ; int ct = (i-j*(3*j+1)/2); if(t < 0&& ct<0 ) break; if(t>=0){ f[i]=(f[i] + flag*f[t]) % mod; } if(ct>=0){ f[i]=(f[i]+flag*f[ct]) % mod ; } } f[i] = (f[i] + mod)% mod ; } } long long calcu(int n,int m) { int flag = -1; long long ans = f[n] ; for(int i=1;;i++){ int t = (i*(3*i-1)/2) ; int ct = (i*(3*i+1)/2); if(t*m<= n){ ans = (ans+ flag*f[n-m*t]) %mod ; } else break; if(ct*m<=n){ ans = (ans+flag*f[n-m*ct]) % mod; } else break; flag*=-1; } ans= (ans + mod) %mod; return ans; } int main() { dabiao() ; int t; scanf("%d",&t) ; while(t--){ int n , m; scanf("%d%d",&n,&m); cout<<calcu(n,m)<<endl; } return 0; }
标签:
原文地址:http://www.cnblogs.com/Scale-the-heights/p/4711643.html