标签:
一、链表
链表结构可以克服数组链表需要预先知道数据大小的缺点,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。(摘自百度)
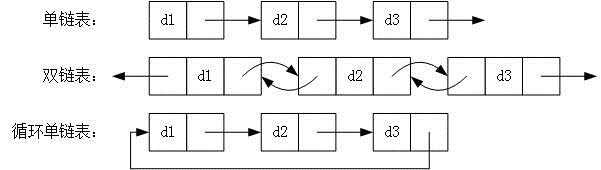
链表结构图:
链表的C语言描述(摘自 数据结构C语言版-严蔚敏):
描述单链表:
1 typedef struct Lnode 2 { ElemType data; /*数据域,保存结点的值 */ 3 struct Lnode *next; /*指针域*/ 4 }LNode; /*结点的类型 */
建立单链表:头插法:
1 LNode *create_LinkList(void) 2 /* 头插入法创建单链表,链表的头结点head作为返回值 */ 3 { int data ; 4 LNode *head, *p; 5 head= (LNode *) malloc( sizeof(LNode)); 6 head->next=NULL; /* 创建链表的表头结点head */ 7 while (1) 8 { scanf(“%d”, &data) ; 9 if (data==32767) break ; 10 p= (LNode *)malloc(sizeof(LNode)); 11 p–>data=data; /* 数据域赋值 */ 12 p–>next=head–>next ; head–>next=p ; 13 /* 钩链,新创建的结点总是作为第一个结点 */ 14 } 15 return (head); 16 }
建立链表:尾插法:
1 LNode *create_LinkList(void) 2 /* 尾插入法创建单链表,链表的头结点head作为返回值 */ 3 { int data ; 4 LNode *head, *p, *q; 5 head=p=(LNode *)malloc(sizeof(LNode)); 6 p->next=NULL; /* 创建单链表的表头结点head */ 7 while (1) 8 { scanf(“%d”,& data); 9 if (data==32767) break ; 10 q= (LNode *)malloc(sizeof(LNode)); 11 q–>data=data; /* 数据域赋值 */ 12 q–>next=p–>next; p–>next=q; p=q ; 13 /*钩链,新创建的结点总是作为最后一个结点*/ 14 } 15 return (head); 16 }
查找节点(按值查找):
1 LNode *Locate_Node(LNode *L,int key) 2 /* 在以L为头结点的单链表中查找值为key的第一个结点 */ 3 { LNode *p=L–>next; 4 while ( p!=NULL&& p–>data!=key) p=p–>next; 5 if (p–>data==key) return p; 6 else 7 { printf(“所要查找的结点不存在!!\n”); 8 retutn(NULL); 9 } 10 }
插入节点(在第i位置插入值为e的节点):
1 void Insert_LNode(LNode *L,int i,ElemType e) 2 /* 在以L为头结点的单链表的第i个位置插入值为e的结点 */ 3 { int j=0; LNode *p,*q; 4 p=L–>next ; 5 while ( p!=NULL&& j<i-1) 6 { p=p–>next; j++; } 7 if (j!=i-1) printf(“i太大或i为0!!\n ”); 8 else 9 { q=(LNode *)malloc(sizeof(LNode)); 10 q–>data=e; q–>next=p–>next; 11 p–>next=q; 12 } 13 }
删除节点(按序号):
1 void Delete_LinkList(LNode *L, int i) 2 /* 删除以L为头结点的单链表中的第i个结点 */ 3 { int j=1; LNode *p,*q; 4 p=L; q=L->next; 5 while ( p->next!=NULL&& j<i) 6 { p=q; q=q–>next; j++; } 7 if (j!=i) printf(“i太大或i为0!!\n ”); 8 else 9 { p–>next=q–>next; free(q); } 10 }
删除节点(按值):
1 void Delete_LinkList(LNode *L,int key) 2 /* 删除以L为头结点的单链表中值为key的第一个结点 */ 3 { LNode *p=L, *q=L–>next; 4 while ( q!=NULL&& q–>data!=key) 5 { p=q; q=q–>next; } 6 if (q–>data==key) 7 { p->next=q->next; free(q); } 8 else 9 printf(“所要删除的结点不存在!!\n”); 10 }
删除节点(删除所有值为key的节点):
思路:从单链表的第一个结点开始,对每个结点进行检查,若结点的值为key,则删除之,然后检查下一个结点,直到所有的结点都检查。
1 void Delete_LinkList_Node(LNode *L,int key) 2 /* 删除以L为头结点的单链表中值为key的第一个结点 */ 3 { LNode *p=L, *q=L–>next; 4 while ( q!=NULL) 5 { if (q–>data==key) 6 { p->next=q->next; free(q); q=p->next; } 7 else 8 { p=q; q=q–>next; } 9 } 10 }
删除节点(删除所有重复节点):
基本思路:从单链表的第一个结点开始,对每个结点进行检查:检查链表中该结点的所有后继结点,只要有值和该结点的值相同,则删除之;然后检查下一个结点,直到所有的结点都检查。
1 void Delete_Node_value(LNode *L) 2 /* 删除以L为头结点的单链表中所有值相同的结点 */ 3 { LNode *p=L->next, *q, *ptr; 4 while ( p!=NULL) /* 检查链表中所有结点 */ 5 { *q=p, *ptr=p–>next; 6 /* 检查结点p的所有后继结点ptr */ 7 while (ptr!=NULL) 8 { if (ptr–>data==p->data) 9 { q->next=ptr->next; free(ptr); 10 ptr=q->next; } 11 else { q=ptr; ptr=ptr–>next; } 12 } 13 p=p->next ; 14 } 15 } 16
双向链表
定义:
指的是构成链表的每个结点中设立两个指针域:一个指向其直接前趋的指针域prior,一个指向其直接后继的指针域next。这样形成的链表中有两个方向不同的链,故称为双向链表。
双向链表是为了克服单链表的单向性的缺陷而引入的。
单个节点:

C语言描述:
1 typedef struct Dulnode 2 { ElemType data ; 3 struct Dulnode *prior , *next ; 4 }DulNode ;
双链表基本操作:
插入:
结构图过程描述

1.插入时仅仅指出直接前驱结点,钩链时必须注意先后次序是: “先右后左” 。
C语言描述:
1 S=(DulNode *)malloc(sizeof(DulNode)); 2 S->data=e; 3 S->next=p->next; p->next->prior=S; 4 p->next=S; S->prior=p; /* 钩链次序非常重要 */
2.插入时同时指出直接前驱结点p和直接后继结点q,钩链时无须注意先后次序。部分语句组如下:
1 S=(DulNode *)malloc(sizeof(DulNode)); 2 S->data=e; 3 p->next=S; S->next=q; 4 S->prior=p; q->prior=S;
删除:
在双向链表中插入和删除必须同时修改两个方向上的指针域的指向。
p->prior->next=p->next; p->next->prior=p->prior; free(p);
二叉树
定义:
二叉树(Binary tree)是n(n≥0)个结点的有限集合。若n=0时称为空树,否则:
⑴ 有且只有一个特殊的称为树的根(Root)结点;
⑵ 若n>1时,其余的结点被分成为二个互不相交的子集T1,T2,分别称之为左、右子树,并且左、右子树又都是二叉树。
由此可知,二叉树的定义是递归的。
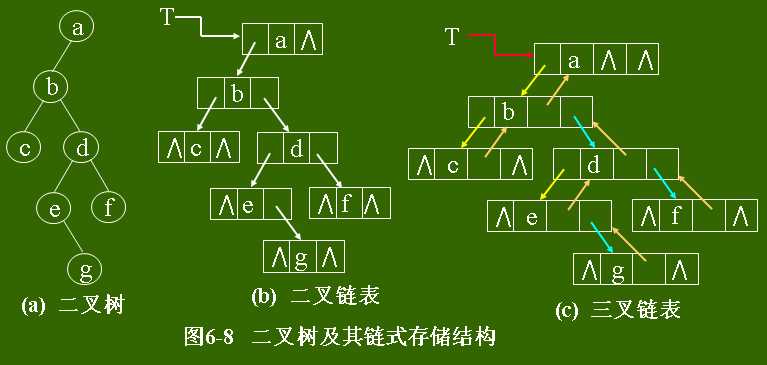
存储结构(链式,这里不讨论顺序存储结构):
C语言描述:
1 typedef struct BTNode 2 { ElemType data ; 3 struct BTNode *Lchild , *Rchild ; 4 }BTNode ;
三叉链表结构:除二叉链表的三个域外,再增加一个指针域,用来指向结点的父结点
结构图:

C语言描述:
1 typedef struct BTNode_3 2 { ElemType data ; 3 struct BTNode_3 *Lchild , *Rchild , *parent ; 4 }BTNode_3 ;
二叉树的链式存储结构:
二叉树的遍历:
若以L、D、R分别表示遍历左子树、遍历根结点和遍历右子树,则有六种遍历方案:DLR、LDR、LRD、DRL、RDL、RLD。若规定先左后右,则只有前三种情况三种情况,分别是:
DLR——先(根)序遍历。
LDR——中(根)序遍历。
LRD——后(根)序遍历。
如图所示的二叉树表示表达式:(a+b*(c-d)-e/f)
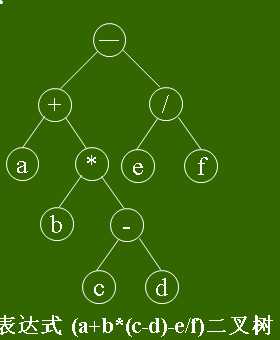
按不同的次序遍历此二叉树,将访问的结点按先后次序排列起来的次序是:
其先序序列为: -+a*b-cd/ef
其中序序列为: a+b*c-d-e/f
其后序序列为: abcd-*+ef/-
先序遍历(递归):
算法的递归定义是:
若二叉树为空,则遍历结束;否则
⑴ 访问根结点;
⑵ 先序遍历左子树(递归调用本算法);
⑶ 先序遍历右子树(递归调用本算法)。
1 void PreorderTraverse(BTNode *T) 2 { if (T!=NULL) 3 { visit(T->data) ; /* 访问根结点 */ 4 PreorderTraverse(T->Lchild) ; 5 PreorderTraverse(T->Rchild) ; 6 } 7 }
说明:visit()函数是访问结点的数据域,其要求视具体问题而定。
先序遍历(非递归):
设T是指向二叉树根结点的指针变量,非递归算法是:
若二叉树为空,则返回;否则,令p=T;
⑴ 访问p所指向的结点;
⑵ q=p->Rchild ,若q不为空,则q进栈;
⑶ p=p->Lchild ,若p不为空,转(1),否则转(4);
⑷ 退栈到p ,转(1),直到栈空为止。
1 #define MAX_NODE 50 2 void PreorderTraverse( BTNode *T) 3 { BTNode *Stack[MAX_NODE] ,*p=T, *q ; 4 int top=0 ; 5 if (T==NULL) printf(“ Binary Tree is Empty!\n”) ; 6 else { do 7 { visit( p-> data ) ; q=p->Rchild ; 8 if ( q!=NULL ) stack[++top]=q ; 9 p=p->Lchild ; 10 if (p==NULL) { p=stack[top] ; top-- ; } 11 } 12 while (p!=NULL) ; 13 } 14 }
中序遍历(递归)
算法的递归定义是:
若二叉树为空,则遍历结束;否则
⑴ 中序遍历左子树(递归调用本算法);
⑵ 访问根结点;
⑶ 中序遍历右子树(递归调用本算法)。
1 void InorderTraverse(BTNode *T) 2 { if (T!=NULL) 3 { InorderTraverse(T->Lchild) ; 4 visit(T->data) ; /* 访问根结点 */ 5 InorderTraverse(T->Rchild) ; 6 } 7 } /*图6-8(a) 的二叉树,输出的次序是: cbegdfa */
中序遍历(非递归)
设T是指向二叉树根结点的指针变量,非递归算法是:
若二叉树为空,则返回;否则,令p=T
⑴ 若p不为空,p进栈, p=p->Lchild ;
⑵ 否则(即p为空),退栈到p,访问p所指向的结点;
⑶ p=p->Rchild ,转(1);
直到栈空为止。
1 #define MAX_NODE 50 2 void InorderTraverse( BTNode *T) 3 { BTNode *Stack[MAX_NODE] ,*p=T ; 4 int top=0 , bool=1 ; 5 if (T==NULL) printf(“ Binary Tree is Empty!\n”) ; 6 else { do 7 { while (p!=NULL) 8 { stack[++top]=p ; p=p->Lchild ; } 9 if (top==0) bool=0 ; 10 else { p=stack[top] ; top-- ; 11 visit( p->data ) ; p=p->Rchild ; } 12 } while (bool!=0) ; 13 } 14 }
后序遍历(递归)
算法的递归定义是:
若二叉树为空,则遍历结束;否则
⑴ 后序遍历左子树(递归调用本算法);
⑵ 后序遍历右子树(递归调用本算法) ;
⑶ 访问根结点 。
1 void PostorderTraverse(BTNode *T) 2 { if (T!=NULL) 3 { PostorderTraverse(T->Lchild) ; 4 PostorderTraverse(T->Rchild) ; 5 visit(T->data) ; /* 访问根结点 */ 6 } 7 } /*图6-8(a) 的二叉树,输出的次序是: cgefdba */
遍历二叉树的算法中基本操作是访问结点,因此,无论是哪种次序的遍历,对有n个结点的二叉树,其时间复杂度均为O(n) 。
后续遍历(非递归)
在后序遍历中,根结点是最后被访问的。因此,在遍历过程中,当搜索指针指向某一根结点时,不能立即访问,而要先遍历其左子树,此时根结点进栈。当其左子树遍历完后再搜索到该根结点时,还是不能访问,还需遍历其右子树。所以,此根结点还需再次进栈,当其右子树遍历完后再退栈到到该根结点时,才能被访问。
因此,设立一个状态标志变量tag :

其次,设两个堆栈S1、S2 ,S1保存结点,S2保存结点的状态标志变量tag 。S1和S2共用一个栈顶指针。
设T是指向根结点的指针变量,非递归算法是:
若二叉树为空,则返回;否则,令p=T;
⑴ 第一次经过根结点p,不访问:
p进栈S1 , tag 赋值0,进栈S2,p=p->Lchild 。
⑵ 若p不为空,转(1),否则,取状态标志值tag :
⑶ 若tag=0:对栈S1,不访问,不出栈;修改S2栈顶元素值(tag赋值1) ,取S1栈顶元素的右子树,即p=S1[top]->Rchild ,转(1);
⑷ 若tag=1:S1退栈,访问该结点;
直到栈空为止。
C语言描述(后续遍历非递归):
1 #define MAX_NODE 50 2 void PostorderTraverse( BTNode *T) 3 { BTNode *S1[MAX_NODE] ,*p=T ; 4 int S2[MAX_NODE] , top=0 , bool=1 ; 5 if (T==NULL) printf(“Binary Tree is Empty!\n”) ; 6 else { do 7 { while (p!=NULL) 8 { S1[++top]=p ; S2[top]=0 ; 9 p=p->Lchild ; 10 } 11 if (top==0) bool=0 ; 12 else if (S2[top]==0) 13 { p=S1[top]->Rchild ; S2[top]=1 ; } 14 else 15 { p=S1[top] ; top-- ; 16 visit( p->data ) ; p=NULL ; 17 /* 使循环继续进行而不至于死循环 */ } 18 } while (bool!=0) ; 19 } 20 }
层次遍历:
层次遍历二叉树,是从根结点开始遍历,按层次次序“自上而下,从左至右”访问树中的各结点。
为保证是按层次遍历,必须设置一个队列,初始化时为空。
设T是指向根结点的指针变量,层次遍历非递归算法是:
若二叉树为空,则返回;否则,令p=T,p入队;
⑴ 队首元素出队到p;
⑵访问p所指向的结点;
⑶将p所指向的结点的左、右子结点依次入队。直到队空为止。
C语言描述(层次遍历非递归):
1 #define MAX_NODE 50 2 void LevelorderTraverse( BTNode *T) 3 { BTNode *Queue[MAX_NODE] ,*p=T ; 4 int front=0 , rear=0 ; 5 if (p!=NULL) 6 { Queue[++rear]=p; /* 根结点入队 */ 7 while (front<rear) 8 { p=Queue[++front]; visit( p->data ); 9 if (p->Lchild!=NULL) 10 Queue[++rear]=p; /* 左结点入队 */ 11 if (p->Rchild!=NULL) 12 Queue[++rear]=p; /* 左结点入队 */ 13 } 14 } 15 }
标签:
原文地址:http://www.cnblogs.com/fysola/p/4712865.html