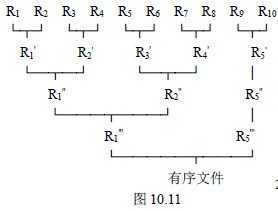
假设有一个含10000 个记录的文件,首先通过10 次内部排序得到10 个初始归并段R1~R10 ,其中每一段都含1000 个记录。然后对它们作如图10.11 所示的两两归并,直至得到一个有序文件为止 如下图
胜者进入下一轮,直至决出本次比赛的冠军。决出冠军之后,充分利用上一次比赛的结果,使得更快地挑出亚军、第三名 …… 。
示例:我们这里以四路归并为例,假设每个归并段已经在输入缓冲区如下图。
每路的第一个元素为胜利树的叶子节点,(5,7)比较出5胜出成为其根节点,(29,9)比较9胜出成为其根节点,一次向上生成一棵胜利树,然后我们可以得出5为冠军,将第一路归并段的元素5放入输出缓冲区,然后将第一路第二个元素放到胜利树中如下:
由第一次得到的胜利树知,我们这里只改变了第1路的叶子节点,所有根节点7的右子树不用再比较,(16,7)比较7胜出,然后7和右子树的胜利者比较7胜出得到亚军,只进行了2次比较。
所以我们知道:
决出第一名需比较: k - 1 次
决出第二名需比较: ![]() 次
次
决出第三名需比较: ![]() 次 .............
次 .............
2.2 败者树
与胜利树相类似,败者树是在双亲节点中记录下刚刚进行完的这场比赛的败者,让胜者去参加更高一层的比赛。
示例:我们这里以四路归并为例,假设每个归并段已经在输入缓冲区如下图。
每路的第一个元素为胜利树的叶子节点,(5,7)比较出5胜出7失败成为其根节点,(29,9)比较9胜出29失败成为其根节点,胜者(5,9)进行下次的比赛7失败成为其根节点5胜出输出到输出缓冲区。由第一路归并段输出,所有将第一路归并段的第二个元素加到叶子节点如下图:
加入叶子节点16进行第二次的比较,跟胜利树一样,由于右子树叶子节点没有发生变化其右子树不用再继续比较。
2.3 败者树程序实现
在创建败者树的时候初始化b[...]和ls[...],b[0]~b[k-1]为k路的第一个元素,即为败者树的叶子节点,ls[0]~ls[k-1]存储的为每次比赛的失败者。
/**
* 已知b[0]到b[k-1]为完全二叉树ls的叶子结点,存有k个关键字,沿从叶子
* 到根的k条路径将ls调整成为败者树。
*/
void CreateLoserTree(LoserTree ls){
int i;
b[k] = MINKEY;
/* 设置ls中“败者”的初值 */
for(i = 0; i < k; ++i){
ls[i] = k;
}
/* 依次从b[k-1],b[k-2],…,b[0]出发调整败者 */
for(i = k - 1; i >= 0; --i){
Adjust(ls, i);
}
}
/* 沿从叶子结点b[s]到根结点ls[0]的路径调整败者树。*/
void Adjust(LoserTree ls, int s){
int i, t;
/* ls[t]是b[s]的双亲结点 */
t = (s + k) / 2;
while(t > 0){
/* s指示新的胜者 */
if(b[s] > b[ls[t]]){
i = s;
s = ls[t];
ls[t] = i;
}
t = t / 2;
}
ls[0] = s;
}
第一次调整:
由程序可以,先找到叶子节点的父节点,t = (s + k) / 2 = 3 ; (s为3),
while(t > 0){
/* s指示新的胜者 */
if(b[s] > b[ls[t]]){
i = s;
s = ls[t];
ls[t] = i;
}
t = t / 2;
}
b[ls[t=3]] = b[k] = MINKEY < b[s] = b[3] 则交换ls[t]=k和s=3,然后t除以2,t/2 = 1, b[ls[1]] = b[k] = MINKEY ,b[s=k]=MINKEY,直到跳出循环,然后 ls[0] = s; 由于ls[0] = s = k,所有不变;
由第二路归并树程序进入调整函数,找到父节点为3,然后就是b[2]和b[3]比较,b[3] = 9胜出,则留在ls[3] = 2,进入下一层的为ls[1] = 3;
由第一路归并树进入调整函数,找到父节点为2,然后是b[1]和b[k=4]比较由于b[4]为最小值,所有b[4]胜出,b[1]失败留在父节点ls[2] = 1,胜者进入上一层与ls[1]比较,很明显b[4]为最小值胜出到达ls[0],留在ls[1] = 3;
由第一路归并树进入调整树,先找到父节点2,然后与父节点比较b[0]胜出,b[1]依旧留在ls[2],继续上一层的比较直到为上图为止。
我们通过对创建败者树的分析可以知道,程序利用初始化败者树全为第k路,一个不存在的一路归并树,并且置第k路的值b[k]为最小值,这是为了让它在每次比较中都能胜出,让第一次比较的值留在失败者的位置,第二次比较的时候自然就跟下一路比较了,这样设计可以减少程序设计的特殊性,避免了特殊情况的出现。创建好败者树后,就可以利用败者树的性质来进行判断了。
实现代码:(为了防止归并段变为空的情况,我们将每路归并段最后都加入 了一个最大元素)
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define MINKEY -1
#define MAXKEY 100
/* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef int Status;
/* Boolean是布尔类型,其值是TRUE或FALSE */
typedef int Boolean;
/* 一个用作示例的小顺序表的最大长度 */
#define MAXSIZE 20
typedef int KeyType;
/* k路归并 */
#define k 3
/* 设输出M个数据换行 */
#define M 10
/* k+1个文件指针(fp[k]为大文件指针),全局变量 */
FILE *fp[k + 1];
/* 败者树是完全二叉树且不含叶子,可采用顺序存储结构 */
typedef int LoserTree[k];
typedef KeyType ExNode, External[k+1];
/* 全局变量 */
External b;
/* 从第i个文件(第i个归并段)读入该段当前第1个记录的关键字到外结点 */
int input(int i, KeyType *a){
int j = fscanf(fp[i], "%d ", a);
if(j > 0){
printf("%d\n", *a);
return 1;
}else{
return 0;
}
}
/* 将第i个文件(第i个归并段)中当前的记录写至输出归并段 */
void output(int i){
fprintf(fp[k], "%d ", b[i]);
}
/* 沿从叶子结点b[s]到根结点ls[0]的路径调整败者树。*/
void Adjust(LoserTree ls, int s){
int i, t;
/* ls[t]是b[s]的双亲结点 */
t = (s + k) / 2;
while(t > 0){
/* s指示新的胜者 */
if(b[s] > b[ls[t]]){
i = s;
s = ls[t];
ls[t] = i;
}
t = t / 2;
}
ls[0] = s;
}
/**
* 已知b[0]到b[k-1]为完全二叉树ls的叶子结点,存有k个关键字,沿从叶子
* 到根的k条路径将ls调整成为败者树。
*/
void CreateLoserTree(LoserTree ls){
int i;
b[k] = MINKEY;
/* 设置ls中“败者”的初值 */
for(i = 0; i < k; ++i){
ls[i] = k;
}
/* 依次从b[k-1],b[k-2],…,b[0]出发调整败者 */
for(i = k - 1; i >= 0; --i){
Adjust(ls, i);
}
}
/**
* 利用败者树ls将编号从0到k-1的k个输入归并段中的记录归并到输出归并段。
* b[0]至b[k-1]为败者树上的k个叶子结点,分别存放k个输入归并段中当前记录的关键字。
*/
void K_Merge(LoserTree ls, External b){
int i, q;
/* 分别从k个输入归并段读人该段当前第一个记录的关键字到外结点 */
for(i = 0; i < k; ++i) {
input(i, &b[i]);
}
/* 建败者树ls,选得最小关键字为b[ls[0]].key */
CreateLoserTree(ls);
while(b[ls[0]] != MAXKEY){
/* q指示当前最小关键字所在归并段 */
q = ls[0];
/* 将编号为q的归并段中当前(关键字为b[q].key)的记录写至输出归并段 */
output(q);
/* 从编号为q的输入归并段中读人下一个记录的关键字 */
if(input(q, &b[q]) > 0){
/* 调整败者树,选择新的最小关键字 */
Adjust(ls,q);
}
}
/* 将含最大关键字MAXKEY的记录写至输出归并段 */
output(ls[0]);
}
void show(KeyType t) {
printf("(%d)", t);
}
int main(){
KeyType r;
int i, j;
char fname[k][4], fout[5] = "out", s[3];
LoserTree ls;
/* 依次打开f0,f1,f2,…,k个文件 */
for(i = 0; i < k; i++){
/* 生成k个文件名f0,f1,f2,… */
itoa(i, s, 10);
strcpy(fname[i], "f");
strcat(fname[i], s);
/* 以读的方式打开文件f0,f1,… */
fp[i] = fopen(fname[i], "r");
printf("有序子文件f%d的记录为:\n",i);
/* 依次将f0,f1,…的数据读入r */
do{
j = fscanf(fp[i], "%d ", &r);
/* 输出r的内容 */
if(j == 1){
show(r);
}
}while(j == 1);
printf("\n");
/* 使fp[i]的指针重新返回f0,f1,…的起始位置,以便重新读入内存 */
rewind(fp[i]);
}
/* 以写的方式打开大文件fout */
fp[k] = fopen(fout, "w");
/* 利用败者树ls将k个输入归并段中的记录归并到输出归并段,即大文件fout */
K_Merge(ls, b);
/* 关闭文件f0,f1,…和文件fout */
for(i = 0; i <= k; i++){
fclose(fp[i]);
}
/* 以读的方式重新打开大文件fout验证排序 */
fp[k] = fopen(fout, "r");
printf("排序后的大文件的记录为:\n");
i = 1;
do{
/* 将fout的数据读入r */
j = fscanf(fp[k], "%d ", &r);
/* 输出r的内容 */
if(j == 1){
show(r);
}
/* 换行 */
if(i++ % M == 0){
printf("\n");
}
}while(j == 1);
printf("\n");
/* 关闭大文件fout */
fclose(fp[k]);
return 0;
}
测试数据:注意在每个文件后面都应该加一个哨兵,即一个最大值
f0: 10 15 16 100
f1: 9 18 20 100
f2: 20 22 40 100
out: 9 10 15 16 18 20 20 22 40 100
参考文献:
[1] http://baike.baidu.com/view/1368718.htm
[2] http://blog.csdn.net/nomad2/archive/2007/12/15/1940266.aspx









