标签:map labeler poj 2296 二分+2-sat
|
Language:
Map Labeler
Description
Map generation is a difficult task in cartography. A vital part of such task is automatic labeling of the cities in a map; where for each city there is text label to be attached to its location, so that no two labels overlap. In this problem, we are concerned
with a simple case of automatic map labeling.
Assume that each city is a point on the plane, and its label is a text bounded in a square with edges parallel to x and y axis. The label of each city should be located such that the city point appears exactly in the middle of the top or bottom edges of the label. In a good labeling, the square labels are all of the same size, and no two labels overlap, although they may share one edge. Figure 1 depicts an example of a good labeling (the texts of the labels are not shown.) Given the coordinates of all city points on the map as integer values, you are to find the maximum label size (an integer value) such that a good labeling exists for the map. 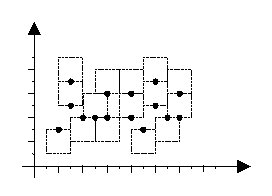 Input
The first line contains a single integer t (1 <= t <= 10), the number of test cases. Each test case starts with a line containing an integer m (3 ≤ m ≤ 100), the number of cities followed by m lines of data each containing a pair of integers; the first integer
(X) is the x and the second one (Y) is the y coordinates of one city on the map (-10000 ≤X, Y≤ 10000). Note that no two cities have the same (x, y) coordinates.
Output
The output will be one line per each test case containing the maximum possible label size (an integer value) for a good labeling.
Sample Input 1 6 1 1 2 3 3 2 4 4 10 4 2 5 Sample Output 2 Source |
题意:平面上有n个点,每个点画一个正方形并且该点要落在正方形上边或者下边的中间,问满足条件的最大正方形的边长是多少。
思路:二分边长mid,建图用2-SAT作为判断条件。
i表示画在上面,~i表示画在下面
if|xi-xj|>=mid continue;
else if |yi-yj|>=2*mid continue;
else if |yi-yj|==0 then i->~j,~i->j,j->~i,~j->i;
else if |yi-yj|>0 then ~i->i,j->~j;
else |yi-yj|>=mid then j->i,~i->~j;
代码:
#include <iostream>
#include <functional>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <string>
#include <map>
#include <stack>
#include <vector>
#include <set>
#include <queue>
#pragma comment (linker,"/STACK:102400000,102400000")
#define pi acos(-1.0)
#define eps 1e-6
#define lson rt<<1,l,mid
#define rson rt<<1|1,mid+1,r
#define FRE(i,a,b) for(i = a; i <= b; i++)
#define FREE(i,a,b) for(i = a; i >= b; i--)
#define FRL(i,a,b) for(i = a; i < b; i++)
#define FRLL(i,a,b) for(i = a; i > b; i--)
#define mem(t, v) memset ((t) , v, sizeof(t))
#define sf(n) scanf("%d", &n)
#define sff(a,b) scanf("%d %d", &a, &b)
#define sfff(a,b,c) scanf("%d %d %d", &a, &b, &c)
#define pf printf
#define DBG pf("Hi\n")
typedef long long ll;
using namespace std;
#define INF 0x3f3f3f3f
#define mod 1000000009
const int maxn = 1005;
const int MAXN = 2005;
const int MAXM = 20010;
const int N = 1005;
struct Node
{
int x,y;
}node[MAXN];
struct Edge
{
int to,next;
}edge[MAXM];
int tot,head[MAXN];
int Low[MAXN],DFN[MAXN],Stack[MAXN],Belong[MAXN];
bool Instack[MAXN];
int top,scc,Index;
void init()
{
tot=0;
memset(head,-1,sizeof(head));
}
void addedge(int u,int v)
{
edge[tot].to=v;
edge[tot].next=head[u];
head[u]=tot++;
}
void Tarjan(int u)
{
int v;
Low[u]=DFN[u]=Index++;
Instack[u]=true;
Stack[top++]=u;
for (int i=head[u];~i;i=edge[i].next)
{
int v=edge[i].to;
if (!DFN[v])
{
Tarjan(v);
if (Low[u]>Low[v]) Low[u]=Low[v];
}
else if (Instack[v]&&Low[u]>DFN[v])
Low[u]=DFN[v];
}
if (Low[u]==DFN[u])
{
scc++;
do{
v=Stack[--top];
Instack[v]=false;
Belong[v]=scc;
}while (v!=u);
}
return ;
}
bool solvable(int n)
{
memset(DFN,0,sizeof(DFN));
memset(Instack,false,sizeof(Instack));
top=scc=Index=0;
for (int i=0;i<n;i++)
{
if (!DFN[i])
Tarjan(i);
}
for (int i=0;i<n;i+=2)
{
if (Belong[i]==Belong[i^1])
return false;
}
return true;
}
bool isok(int mid,int n) //根据mid建图
{
init();
for (int i=0;i<n;i++)
{
for (int j=i+1;j<n;j++)
{
if (abs(node[i].x-node[j].x)>=mid) continue;
if (abs(node[i].y-node[j].y)>=2*mid) continue;
if (node[i].y==node[j].y)
{
addedge(2*i,2*j+1);
addedge(2*j+1,2*i);
addedge(2*j,2*i+1);
addedge(2*i+1,2*j);
}
else if (node[i].y-node[j].y>0&&node[i].y-node[j].y<mid)
{
addedge(2*i+1,2*i);
addedge(2*j,2*j+1);
}
else if (node[j].y-node[i].y>0&&node[j].y-node[i].y<mid)
{
addedge(2*j+1,2*j);
addedge(2*i,2*i+1);
}
else if (node[i].y-node[j].y>=mid)
{
addedge(2*i+1,2*j+1);
addedge(2*j,2*i);
}
else if (node[j].y-node[i].y>=mid)
{
addedge(2*j+1,2*i+1);
addedge(2*i,2*j);
}
}
}
if (solvable(2*n)) return true;
return false;
}
void solve(int n) //二分
{
int l=0,r=10000,ans;
while (l<=r)
{
// DBG;
int mid=(l+r)>>1;
if (isok(mid,n))
{
// DBG;
ans=mid;
l=mid+1;
}
else r=mid-1;
}
printf("%d\n",ans);
}
int main()
{
#ifndef ONLINE_JUDGE
freopen("C:/Users/lyf/Desktop/IN.txt","r",stdin);
#endif
int i,j,t,m;
scanf("%d",&t);
while (t--)
{
scanf("%d",&m);
for (i=0;i<m;i++)
scanf("%d%d",&node[i].x,&node[i].y);
solve(m);
}
return 0;
}
版权声明:本文为博主原创文章,未经博主允许不得转载。
Map Labeler (poj 2296 二分+2-SAT)
标签:map labeler poj 2296 二分+2-sat
原文地址:http://blog.csdn.net/u014422052/article/details/47403547