标签:
可以用队列优化或斜率优化的dp这一类的问题为 1D/1D一类问题
即状态数是O(n),决策数也是O(n)
我们来看这样一个问题:一个含有n项的数列(n<=2000000),求出每一项前面的第m个数到它这个区间内的最小值
可以使用RMQ求区间最小值,那么时间复杂度是O(nlogn),不是让人很满意。
dp[i]为i-m+1->i这个区间的最小值。
那么状态转移方程是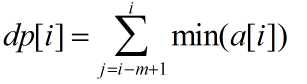
可以看出,这个题目的状态数是O(n),决策数是O(m),且决策的区间是连续的,那么可以尝试想办法把O(m)优化成O(1)
我们可以用单调队列维护一个数据结构,这个数据结构有两个域,pos和val,pos代表下标,val代表该下标所对应的值。队列中的pos单调递增,且val也单调递增
那么当计算一个状态时,只要从队首不断弹出pos<i-m+1的数据,只要pos>=i-m+1,那么该决策就是最优的,因为队列是单调的啊。
同理,同队尾插入一个数据时,只要不断剔除val比a[i]大的数据,直到遇到小于它的,然后将该数据插入队尾。
每个数据只入队列,出队列一次,所以时间复杂度是O(n),
分析:为什么插入的时候,比a[i]大的数据可以剔除,因为j<i时,a[j] > a[i], 那么以后所有的决策中,a[i]都比a[j]更优
为什么可以不断删除pos<i-m+1的数据,因为i是递增的,该数据对当前的i没用,那么对以后的i也是没用的。

1 #include <stdio.h> 2 #include <string.h> 3 #include <stdlib.h> 4 #include <algorithm> 5 #include <iostream> 6 #include <queue> 7 #include <stack> 8 #include <vector> 9 #include <map> 10 #include <set> 11 #include <string> 12 #include <math.h> 13 using namespace std; 14 #pragma warning(disable:4996) 15 #pragma comment(linker, "/STACK:1024000000,1024000000") 16 typedef long long LL; 17 const int INF = 1<<30; 18 /* 19 */ 20 const int N = 100 + 10; 21 int a[N]; 22 int dp[N]; 23 int q[N], head, tail; 24 int main() 25 { 26 int n, m; 27 while (scanf("%d%d", &n,&m) != EOF) 28 { 29 for (int i = 1; i <= n; ++i) 30 scanf("%d", &a[i]); 31 head = tail = 0; 32 q[tail++] = 1; 33 dp[1] = a[1]; 34 for (int i = 2; i <= n; ++i) 35 { 36 while (head < tail && a[i] < a[q[tail - 1]])//插入新的元素,要使得队列依旧单调递增 37 tail--; 38 q[tail++] = i; 39 while (head < tail && q[head] < i - m + 1)//剔除不合要求的pos 40 head++; 41 dp[i] = a[q[head]]; 42 } 43 for (int i = 1; i <= n; ++i) 44 printf("%d ", dp[i]); 45 puts(""); 46 /* 47 5 3 48 1 2 3 4 5 49 1 1 1 2 3 50 */ 51 } 52 return 0; 53 }
那么我们可以抽象出一类模型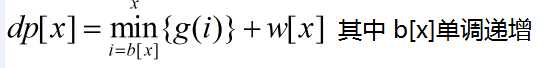
需要注意到,上面要求可选的决策集是连续的。同时也可以注意到,当前决策所需要的值是不受现在的状态所影响的,即g(i)与w[x]是相互独立的。
我们在单调队列的最后说道,当前决策所需要的值是不受现在的状态所影响的,即g(i)与w[x]是相互独立的。
还有的1D/1D一类问题是想下面这样的。
但是如果状态转移方程是这样的: dp[i]=dp[j]+(x[i]-x[j])*(x[i]-x[j]) ,1<=j<=i 把括号化开后,得到2x[i]*x[j], 这使得当前决策所需要的值受当前状态的影响
所以上面单调队列的方法就不行了。
【参考文献】
《1D1D动态规划优化初步》 作者:南京师范大学附属中学 汪一宁
《用单调性优化动态规划》 JSOI2009集训队论文
标签:
原文地址:http://www.cnblogs.com/justPassBy/p/4719207.html