标签:
给定n对括号,生成所有可能的括号组合
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses. For example, given n = 3, a solution set is: "((()))", "(()())", "(())()", "()(())", "()()()"
采用树的方式来选择生成所有的组合结果树,每种组合是树的一个遍历分支。
有两种方法,基本一样的。
第一种,定义三个变量:
其中lLeft<=rLeft始终成立。则有如下判断:
代码如下:

1 public class Solution { 2 List<String> res; 3 public void dfs( String now, int lLeft, int rLeft ){ 4 if( lLeft == 0 ){ 5 char[] rLeftString = new char[rLeft]; 6 for( int i=0; i<rLeft; i++ ) 7 rLeftString[i] = ‘)‘; 8 res.add( now + String.valueOf(rLeftString) ); 9 } 10 else{ 11 dfs( now + "(", lLeft-1, rLeft ); 12 if( lLeft < rLeft ) 13 dfs( now + ")", lLeft, rLeft-1 ); 14 } 15 } 16 17 public List<String> generateParenthesis( int n ){ 18 res = new ArrayList<String>(); 19 dfs( "", n, n ); 20 return res; 21 } 22 }
第二种,定义三个变量:
则有如下判断(以n=3为例,用0代表左括号,1代表右括号):
下图是n=3时的判断实例,其中最左的一个分支是((())),第二个是(()()):
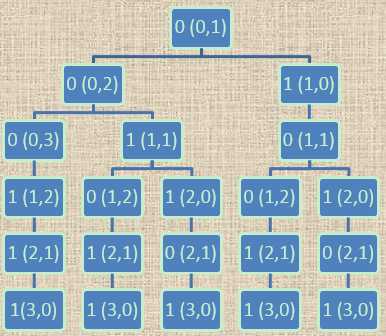
代码如下:

public class Solution { List<String> res; public void expand( String now, int i, int j, int n ){ //finish matching if( i == n ){ res.add( now ); return; } //all left parentheses are used if( i + j == n ) expand( now + ")", i+1, j-1, n ); //there‘re still unused left parentheses else{ //there‘re still unmatched left parentheses if( j > 0 ){ expand( now + "(", i, j+1, n ); expand( now + ")", i+1, j-1, n ); } //all used left parentheses are matched at present else if( j == 0 ) expand( now + "(", i, j+1, n ); } } public List<String> generateParenthesis( int n ){ res = new ArrayList<String>(); expand( "(", 0, 1, n ); return res; } }
标签:
原文地址:http://www.cnblogs.com/hf-cherish/p/4668988.html