标签:
POJ3739 Special Squares
描述:
There are some points and lines parellel to x-axis or y-axis on the plane. If arbitrary chosen two lines parallel to x-axis and two lines parallel to y-axis, one rectangle, or sometimes a square, will be formed. If a square is formed and there is one or more point in the square or on the side of the square, the square is called a "special square". Please find the number of special squares.
输入:
The 1st line contains three positive integer n1, n2 and n3. n1 stands for the number of lines parallel to x-axis, n2 stands for the number of lines parallel to y-axis, n3 stands for the number of points.(0<n1, n2, n3≤1000)
Each of the 2nd line to (n1+1)th line gives an integer y_i (0≤y_i≤1000), means a line with equation y=y_i.
Each of the (n1+2)th line to (n1+n2+1)th line
gives an integer x_j (0≤x_j≤1000), means a line with equation x=x_j.
Each of the last three lines gives two integers px_k and py_k
(0≤px_k,py_k≤1000), means a point with coordinate (px_k, py_k).
输出:
Output one line containing an integer specifies the number of special squares. The test data ensures that the result is less than 2^31
样例输入:
4 4 3
0 2 4 6
0 2 4 6
1 1
3 3
6 6
样例输出
8
题目分析:
本题大意是输入一些平行于x轴,y轴的直线,和一些点,输出由这些线组成的包含有点的正方形的个数。
这是一道区域覆盖的题。本题的难点有两处:1.如何判断并统计出所有正方形(不是长方形),2.如何判断这些正方形是否包含点。
我的思路就是统计出所有的正方形,然后逐个遍历,判断其是否包含点。
第一步,对点进行预处理,统计点(0,0)到点(i,j)之间的点的个数,
第二步,讲题目中的各横纵坐标值往X轴45度投影,得到所有已知直线交叉得到的点,并将其存储在一个点数组向量中。
点数组向量v[i]中存储了第i列对角线上的交叉点。
第三部,遍历正方形,判断其是否含点。
由于点存储在点向量数组v中,故遍历这些对角线上的点即可组成正方形,如下图所示:
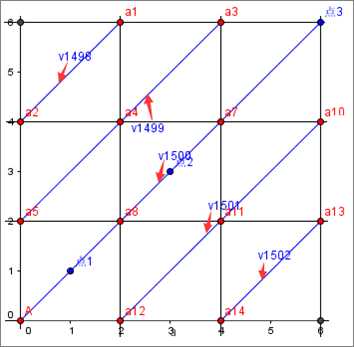
该图是根据样例数据画的图,蓝点代表样例给的点,另各平行线及其交点如图,交点用红色点表示,a1...a14
其中,点数组向量v[1498]中存放了点a1、a2;v[1499]中存放了点a3、a4、a5 ..... v[1502]中存放了点a13、a14。
第四步,用对角线表示其所在的对角线。其包含点的求法为,例:a7a6 = a9a6 - a9a10 - a9a3 +a9a7。(a9为原点,a6为点3)
代码如下:
1 #include<stdio.h> 2 #include<vector> 3 #include<algorithm> 4 using namespace std; 5 6 struct point{ 7 int x; 8 int y; 9 }; 10 11 vector<point> v[3002]; 12 int n1,n2,n3,x[1500],y[1500],p[1500][1500]; //p[][]统计在该范围内点的个数 13 bool flag1[1500][1500]; 14 point v1[1500]; 15 16 int cmp(void const *a,void const *b) 17 { 18 return *(int *)a-*(int *)b; 19 } 20 21 int main() 22 { 23 int i,j,k,len,cnt(0),flag,temp1,ii; 24 point temp; 25 26 scanf("%d%d%d",&n1,&n2,&n3); 27 for(i=0;i<n1;i++) scanf("%d",&y[i]); 28 for(i=0;i<n2;i++) scanf("%d",&x[i]); 29 for(i=0;i<n3;i++) 30 { 31 scanf("%d%d",&v1[i].x,&v1[i].y); 32 flag1[v1[i].x][v1[i].y]=1; 33 } 34 35 qsort(y,n1,sizeof(int),cmp); 36 qsort(x,n2,sizeof(int),cmp); 37 38 for(i=0; i<n2; i++) //对点进行预处理 39 for(j=0; j<n1; j++) 40 for(k=0;k<n3;k++) 41 if(v1[k].x<=x[i] && v1[k].y<=y[j]) 42 p[x[i]][y[j]]++; 43 44 for(i=0; i<n2; i++) //把坐标往X轴45度投影,得到所有正方形 45 for(j=0; j<n1; j++) //同一条对角线上的点会存储在1个v[i]中,i表示第i条对角线 46 { 47 len=x[i]-y[j]+1500; 48 temp.x=x[i]; 49 temp.y=y[j]; 50 v[len].push_back(temp); 51 } 52 for(i=0; i<3002; i++) //判断点是否在正方形内 53 for(j=0; j<v[i].size(); j++) //v[i][j] v[i][k] 为正方形左下角右上角顶点 54 { 55 flag=0; 56 for(k=j+1; k<v[i].size(); k++) 57 { 58 ii=0; 59 temp1 = p[v[i][k].x][v[i][k].y] - //temp1为该正方形内点的个数 60 p[v[i][j].x][v[i][k].y] - 61 p[v[i][k].x][v[i][j].y]; 62 if(flag1[v[i][j].x][v[i][k].y] == 1) ii++; //判断 (j.x, j.y) (j.x, k,y) (j.y, k.x) 三点的是否有点存在 63 if(flag1[v[i][k].x][v[i][j].y] == 1) ii++; 64 if(flag1[v[i][j].x][v[i][j].y] == 1) ii++; 65 if(temp1+p[v[i][j].x][v[i][j].y]+ii > 0) 66 { 67 cnt+=v[i].size()-k; 68 flag=1; 69 } 70 if(flag) break; 71 } 72 } 73 printf("%d\n",cnt); 74 return 0; 75 }
标签:
原文地址:http://www.cnblogs.com/Lg-Lee/p/4719749.html