2.5 ESL第二章习题2.5

标签：

题目

描述

• $y_i=x_i^T\beta+\epsilon_i$
  $\epsilon_i\sim N(0,\sigma^2)$

• 已有训练集$\tau$，其中$X:n\times p,y:n\times 1,\epsilon:n\times 1$
  使用最小二乘得到$\hat{\beta}=\left(X^TX\right)^{-1}X^Ty$
  $y=X\beta+\epsilon$

• 需要预测点$x_0$的値$y_0$

题2.7

• 准备

  • $E(y_0)=E(x_0^T\beta+\epsilon_0)=E(x_0^T\beta)+E(\epsilon_0)=x_0^T\beta+0$
  • $E[\left(y_0-E(y_0)\right)^2]=E[\left(x_0^T\beta+\epsilon_0-x_0^T\beta\right)^2]=E[\epsilon_0^2]=\sigma^2$
  • $\hat{y_0}=x_0^T\hat{\beta}=x_0^T\left(X^TX\right)^{-1}X^T\left(X\beta+\epsilon\right)\\ \ =x_0^T\left(X^TX\right)^{-1}X^TX\beta+x_0^T\left(X^TX\right)^{-1}X^T\epsilon\\ \ =x_0^T\beta+x_0^T\left(X^TX\right)^{-1}X^T\epsilon\\ \ =x_0^T\beta+\sum_i a_i\epsilon_i$ <br>其中$a_i=\left[x_0^T\left(X^TX\right)^{-1}X^T\right]_i$
  • $E(\hat{y_0})=E(x_0^T\beta+\sum_i a_i\epsilon_i)=x_0^T\beta+\sum_i E(a_i)E(\epsilon_i)=x_0^T\beta$
    这里由于$X$由某分布产生，所以$E(a_i)$不是简单常数

• 题解

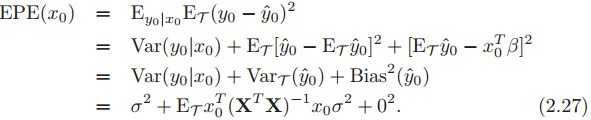
  $EPE(x_0)=\int\int\left(y_0-\hat{y_0}\right)^2p(y_0)p(\hat{y_0})\mathrm{d} y_0\mathrm{d}\hat{y_0}\\ \ =\int\int\left[\hat{y_0}-E(\hat{y_0})+E(\hat{y_0})-y_0\right]^2p(y_0)p(\hat{y_0})\mathrm{d} y_0\mathrm{d}\hat{y_0}\\ \ =\int\left[\hat{y_0}-E(\hat{y_0})\right]^2p(\hat{y_0})\mathrm{d}\hat{y_0}+\int\int\left[E(\hat{y_0})-y_0\right]^2p(y_0)p(\hat{y_0})\mathrm{d} y_0\mathrm{d}\hat{y_0}+2\times 0\\ \ ={Var}_\tau(\hat{y_0})+\int\int\left[y_0-E(y_0)+E(y_0)-E(\hat{y_0})\right]^2p(y_0)p(\hat{y_0})\mathrm{d} y_0\mathrm{d}\hat{y_0}\\ \ ={Var}_\tau(\hat{y_0})+\int\left[y_0-E(y_0)\right]^2p(y_0)\mathrm{d} y_0+\left[E(y_0)-E(\hat{y_0}\right]^2+2\times 0\\ \ ={Var}_\tau(\hat{y_0})+\sigma^2+0^2$
  ${Var}_\tau(\hat{y_0})=E\left[\hat{y_0}-E(\hat{y_0})\right]^2\\ \ =E\left[x_0^T\beta+\sum_i a_i\epsilon_i-x_0^T\beta\right]^2=E\left[\sum_i\sum_j a_ia_j\epsilon_i\epsilon_j\right]\\ \ =E\left[ \sum_i a_i^2\epsilon_i^2 \right]+E\left[\sum_i\sum_{j:j\neq i} a_ia_j\epsilon_i\epsilon_j\right]\\ \ =\sum_iE(a_i^2)E(\epsilon_i^2)+\sum_i\sum_{j:j\neq i} E(a_ia_j)E(\epsilon_i)E(\epsilon_j)\\ \ =\sigma^2E(\sum_i a_i^2)+0=\sigma^2E\left(x_0^T\left(X^TX\right)^{-1}X^TX\left(X^TX\right)^{-1}x_0\right)\\ \ =\sigma^2E\left(x_0^T\left(X^TX\right)^{-1}x_0\right)$

题2.8

• 准备

  • 假设$E(x^{(i)})=0,i=1...p$，即每个维度的期望都为0
    $X^TX$得到$p\times p$的矩阵
    $X_{:i}$表示$X$的第$i$列，即训练集输入部分的第i个维度
    $X_{:i}^TX_{:i}=\sum_j^N {x_j^{(i)}}^2=N\ \frac{1}{N}\sum_j^N (x_j^{(i)}-E(x^{(i)}))^2=N\hat{Var}(x^{(i)})$得到对角元素
    $X_{:i}^TX_{:j}=\sum_t^N x_t^{(i)}x_t^{(j)} = N\ \frac{1}{N} (x_t^{(i)}-E(x^{(i)}))(x_t^{(j)}-E(x^{(j)}))=N\hat{Cov}(x^{(i)},x^{(j)})$
    当$N\to \infty $，$X^TX \to NCov(x)$
  • $K:p\times p,b:p\times 1$
    $trace Kbb^T=\sum_i {[Kbb^T]}_{ii}=\sum_i \sum_j K_{ij}{[bb^T]}_{ji}=\sum_i \sum_j K_{ij}b_ib_j$
    $b^TKb=\sum_i {b^T}_{1i}{[Kb]}_{i1}=\sum_i \sum_j b_iK_{ij}b_j$
    $trace Kbb^T=b^TKb$

• 题解

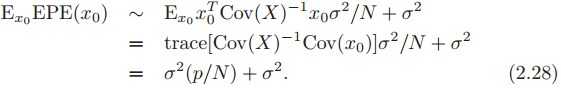
  $E\left(x_0^T\left(X^TX\right)^{-1}x_0\right)\sim E\left(x_0^T{Cov(x)}^{-1}x_0\right)/N\\ \ =E\left(trace {Cov(x)}^{-1}x_0x_0^T\right)/N\\ \ =trace {Cov(x)}^{-1}E(x_0x_0^T)/N=trace {Cov(x)}^{-1}Cov(x)/N\\ \ =trace I/N=p/N$
  $EPE(x_0)=(p/N+1)\sigma^2$

2.5 ESL第二章习题2.5

标签：

原文地址：http://www.cnblogs.com/porco/p/4719741.html