标签：poj   树状数组   

链接：http://poj.org/problem?id=2352

Description

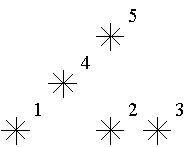
For example, look at the map shown on the figure above. Level of the star number 5 is equal to 3 (it‘s formed by three stars with a numbers 1, 2 and 4). And the levels of the stars numbered by 2 and 4 are 1. At this map there are only one star of the level 0, two stars of the level 1, one star of the level 2, and one star of the level 3.

You are to write a program that will count the amounts of the stars of each level on a given map.

Input

Output

Sample Input

Sample Output

大意——给定一个星座图，星座上的每个星星都有一个笛卡尔坐标。一个星星的等级是等于纵坐标不大于它且横坐标也不大于它的星星的数目。现在给你n个星星以及它们的坐标，坐标是按纵坐标上升的顺序给出的，纵坐标相同则按横坐标上升的顺序给出。要你求出各等级的星星的个数。

思路——因为坐标给出的特点，所以我们只需要求出不大于给定坐标横坐标有几个即可。那么它的等级就等于前面已经输入的横坐标在[0,x]区间的星星数量。于是，我们可以用树状数组来统计个数。

复杂度分析——时间复杂度:O(n*log(x)),空间复杂度:O(x)

附上AC代码：

#include <iostream>
#include <cstdio>
#include <string>
#include <cmath>
#include <iomanip>
#include <ctime>
#include <climits>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <queue>
#include <vector>
#include <set>
#include <map>
using namespace std;
typedef unsigned int UI;
typedef long long LL;
typedef unsigned long long ULL;
typedef long double LD;
const double pi = acos(-1.0);
const double e = exp(1.0);
const double eps = 1e-8;
const int maxn = 32005;
int point[maxn];
int level[maxn];

int lowbit(int x);
void update(int x, int add);
int sum(int x);

int main()
{
	ios::sync_with_stdio(false);
	int n, x, y;
	while (~scanf("%d", &n))
	{
		memset(level, 0, sizeof(level));
		memset(point, 0, sizeof(point));
		for (int i=0; i<n; i++)
		{
			scanf("%d%d", &x, &y);
			level[sum(x+1)]++;
			update(x+1, 1); // 更新节点信息
		}
		for (int i=0; i<n; i++)
			printf("%d\n", level[i]);
	}
	return 0;
}

int lowbit(int x) // 求2^k,k表示x化为二进制时末位的零
{
	return (x&(-x));
}

void update(int x, int add)
{
	while (x!=0 && x<=maxn)
	{
		point[x] += add;
		x += lowbit(x);
	}
}

int sum(int x)
{
	int res = 0;
	while (x > 0)
	{
		res += point[x];
		x -= lowbit(x);
	}
	return res;
}

POJ 2352 Stars

标签：poj   树状数组   

原文地址：http://blog.csdn.net/silenceneo/article/details/47414403