标签:
对于受均布荷载的简支梁,假设梁的长度L=1,均布荷载大小为1,弹模E为1,惯性矩I为1,那么梁的挠曲线方程的解析解为
$$
v(x)=-\left(\frac{x^4}{24}-\frac{x^3}{12}+\frac{x}{24}\right)
$$
梁单元的形函数如下
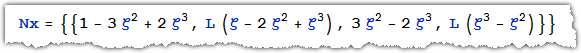
根据形函数的定义,只要知道了单元两端节点的位移,即可用形函数求出单元上任意位置的挠度。即
$$
v(x)=N(x)\cdot q^{e}
$$
其中$q^{e}$为节点的位移列阵。
下面对比一下,由形函数得到的挠度曲线与挠曲线的解析解之间的差别,为了对比方便,这里采用形函数时,节点的位移均由挠曲线解析解求出,换言之,在节点处的位移是精确的。
1.假设将上图结构中梁看作一个单元
$$
\begin{split}
v(0)=0\quad & v‘(0)=-\dfrac{1}{24}\\
v(1)=0\quad & v‘(1)=\dfrac{1}{24}
\end{split}
$$
把形函数行矩阵与上面的节点位移列阵相乘,可以得到挠曲线方程
$$
v1(x)=\frac{x^2}{24}-\frac{x}{24}
$$
2.假设将上图中梁看着2个单元
每个单元的长度L=1/2
利用MM求得挠曲线方程的分段函数为
分别把解析解,1个单元,2个单元求得的挠曲线方程画出来
可以看到,采用2个单元时,挠曲线方程与解析解十分接近,几乎重合;而采用1个单元时,较解析解差别较大。考察在1/4处的数值
| 1/4出挠度值 | |
| 解析解 | -0.00927734 |
| 1个单元 | -0.0078125 |
| 2个单元 | -0.00911458 |
标签:
原文地址:http://www.cnblogs.com/SimuLife/p/4722707.html