标签:









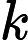

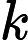









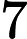



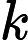



















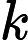


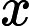


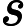
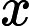

2 3 2 1 2 1 3 10 8 2 1 3 2 4 1 5 3 6 1 7 3 8 7 9 7 10 6
Case #1: 4 Case #2: 316512
可以用求概率的思想来解决这个问题。令以i号节点为根的子树为第i棵子树,设这颗子树恰好有sz[i]个点。那么第i个点是第i棵子树最大值的概率为1/sz[i],不是最大值的概率为(sz[i]-1)/sz[i]。现在可以求解恰好有k个最大值的概率。
令dp[i][j]表示考虑编号从1到i的点,其中恰好有j个点是其子树最大值的概率。 很容易得到如下转移方程:dp[i][j]=dp[i-1][j]*(sz[i]-1)/sz[i]+dp[i-1][j-1]/sz[i]。这样dp[n][k]就是所有点中恰好有k个最大值的概率。
题目要求的是方案数,用总数n!乘上概率就是答案。计算的时候用逆元代替上面的分数即可
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <set>
#define LL long long
using namespace std;
const int MAXN = 1000 + 10;
const int MOD = 1000000000 + 7;
int read()
{
int res = 0, f = 1; char ch = getchar();
while(ch < '0' || ch > '9'){if(ch == '-') f *= -1; ch = getchar();}
while(ch >= '0' && ch <= '9'){res = res * 10 + ch - '0'; ch = getchar();}
return res;
}
int sz[MAXN], vis[MAXN];
int n, k;
LL dp[MAXN][MAXN], inv[MAXN], fac[MAXN];
struct Edge
{
int to, next;
}edge[MAXN<<1];
int tot, head[MAXN];
void init()
{
tot = 0;
for(int i=0;i<=n;i++)
{
head[i] = -1;
vis[i] = 0;
sz[i] = 0;
}
}
void addedge(int u, int v)
{
edge[tot].to = v;
edge[tot].next = head[u];
head[u] = tot++;
}
int dfs(int u, int pre)
{
int ans = 1;vis[u] = 1;
for(int i=head[u];i!=-1;i=edge[i].next)
{
int v = edge[i].to;
if(v == pre) continue;
if(!vis[v]) ans += dfs(v, u);
}
return sz[u] = ans;
}
LL pow_mod(LL a, LL b)
{
LL res = 1;
while(b)
{
if(b & 1) res = res * a % MOD;
a = a * a % MOD;
b >>= 1;
}
return res % MOD;
}
int main()
{
int T, kcase = 1;
for(int i=1;i<MAXN;i++) inv[i] = pow_mod(i, MOD - 2);
fac[0] = 1; for(int i=1;i<MAXN;i++) fac[i] = fac[i-1] * i % MOD;
T = read();
while(T--)
{
n = read(); k = read();
int u, v; init();
for(int i=1;i<n;i++)
{
u = read();v = read();
addedge(u, v);
addedge(v, u);
}
dfs(1, -1);
for(int i=0;i<=n;i++) for(int j=0;j<=k;j++) dp[i][j] = 0;
dp[0][0] = 1;
for(int i=1;i<=n;i++)
{
for(int j=0;j<=k;j++)
{
dp[i][j] = ((dp[i-1][j] * (sz[i] - 1)) % MOD) * inv[sz[i]] % MOD +
dp[i-1][j-1] * inv[sz[i]] % MOD;
}
}
LL ans = (dp[n][k] * fac[n]) % MOD;
printf("Case #%d: %I64d\n", kcase++, ans);
}
return 0;
}版权声明:本文为博主原创文章,未经博主允许不得转载。
HDU 5378 Leader in Tree Land(2015 多校第7场 dp)
标签:
原文地址:http://blog.csdn.net/moguxiaozhe/article/details/47439691