人生的第一道动态树,为了弄懂它的大致原理,需要具备一些前置技能,如Splay树,树链剖分的一些概念。在这里写下一些看各种论文时候的心得,下面的代码是拷贝的CLJ的模板,别人写的模板比较可靠也方便自己学习理解,然后一些概念的则是学习了一些论文,下面的内容可以看作对别人模板的理解心得,以及对论文的收获体会。
LCT支持的主要是一种树路径上的操作,譬如说对u和v之间的路径上询问点权的和,询问点权的最大值,对所有点权加一个数,置为一个树等等。它和树链剖分不同的是,它支持将这个树上的边切掉,也支持将两个树通过连一条边合并。 树链剖分则不支持切边和删边的操作。
树链剖分的方法主要是这样的,对于一棵树,我们先dfs一次求出每个点的重儿子(即儿子里拥有最多点的那个),然后标记这些边为重边(其余为轻边),然后第二次dfs的时候将重边编号,实现了连续的重边具有连续的编号的效果。根据一定的推导可以证明从任意一点到根的路径上的轻边和重边是O(logn)级别的,因此修改路径的时候就可以用线段树去维护边,由于每条边都要维护,每条边更新的代价都是logn,所以单次操作复杂度是log^2n.
LCT具有相同的思想,但由于是动态的,因此就需要更加灵活一点的数据结构,那就是动态树了。重边和轻边的概念也在这里得到一定的应用或者拓展,下面的图截自《SPOJ375 QTREE 解法的一些研究 》
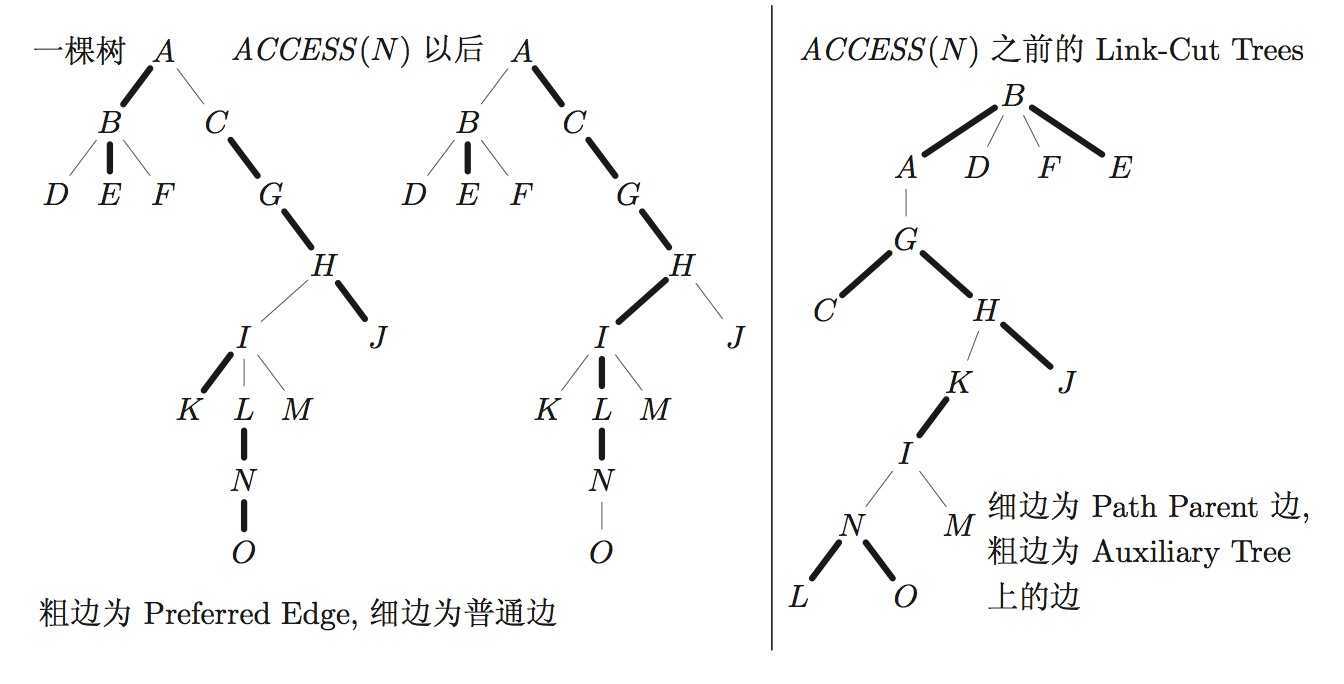
对这幅图的理解我觉得是至关重要的。在LCT里定义了这么一种操作叫做ACCESS,也可以叫做expose,在执行了access(N)之后我们就可以发现,从N到根的路径上的所有边都变成了重边,而且由于每个父亲只有一个重儿子,也只有一条重边,所以原本的重边会变成轻边。
在Splay里维护的是一条条的重链(只有一个点的也是一棵树),每条重链就是一棵Splay树。例如左一、二图里维护的就是下面的一系列Splay树
左一:A-B-E;C-G-H-J;I-K;L-N-O;D;F;M
左二:A-C-G-H-I-L-N;B-E;D;F;J;K;M;O
然后在每一棵Splay树里,左子树的点在当前点的上方,右子树的点在当前点的下方。图三就是对此的一个描述,看C-G-H-J这一条重链,G的左子树有C,说明C在G的上方,同理H,J在G的下方,跟左一图是对应的。
此外重链之间的关系也是要维护的,所以没有加粗的细边起的就是这个作用,反应在Splay树的实现上,就是每个Node里面要多加一个fa,表示的是这条重链的父边在哪里。
接下来就是理解expose的操作了,expose(v)要将v到根上的所有点打到同一条重链上(同一棵Splay树上)具体操作可以看一下上面那篇论文里的伪码,还可以参考一下下面这篇论文里的伪码 《动态序列与动态树问题——浅谈几种常用数据》
然后就是几个典型的操作的问题了,下面就是几个典型操作的主要内容:
(1)寻根:findRoot(u):expose(u),splay(u),while(u->ch[0]!=null) {u=u->ch[0]} splay(u)
其实就是将u到根的路径expose出来,然后splay到根,因为左子树的点一定在最上方,所以就不停地走左子树直到没得走,然后由于是splay树,所以每次操作完也得再splay一次到根
(2)换根:makeRoot(u):expose(u),splay(u),u->revIt();
其实就是将u到根的路径expose出来,然后将u spaly到根,由于expose完u之后u下方必然没有点,可以肯定的是splay(u)之后 u->ch[1]是空的,这个时候再翻转一下就可以将u转到根了,所以Node节点里一定有一个rev标记。
其余的加边,删边,询问,修改也是大同小异的,无非就是将路径expose出来,然后适当的splay一下,进行相应的修改。
代码的实现上和splay差不多,但是要特别注意几个点,一是Node节点类里面新增了一些属性,如isRoot表示是否为根,fa表示轻边的父亲。在旋转的时候要相应的维护好根的情况,在有lazy标记的时候,还要多写一个pushTo的函数将点到根上的所有的标记下传。
代码太长了,实现细节太多了,不对着别人的模板写完全就写不下来嘛,实在是太恐怖了。
#pragma warning(disable:4996)
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <vector>
#include <algorithm>
#include <map>
using namespace std;
#define ll long long
#define maxn 350000
#define INF 0x3f3f3f3f
struct Node
{
Node *p, *ch[2];
bool rev;
ll sum, val;
ll mx;
ll add;
int size;
bool isRoot;
Node *fa;
Node(){
sum = 0; val = 0;
rev = 0; mx = -INF;
add = 0;
size = 0;
}
void setc(Node *c, int d){
ch[d] = c;
c->p = this;
}
bool d(){
return p->ch[1] == this;
}
void upd(){
sum = ch[0]->sum + ch[1]->sum + val;
size = ch[0]->size + ch[1]->size + 1;
mx = max(max(ch[0]->mx, ch[1]->mx), val);
}
void revIt(){
rev ^= 1;
}
void addIt(int vx){
add += vx;
sum += vx*size;
val += vx;
mx += vx;
}
void relax();
void setRoot(Node *f);
}Tnull, *null = &Tnull;
void Node::setRoot(Node *f){
fa = f;
isRoot = true;
p = null;
}
void Node::relax(){
if (add != 0){
for (int i = 0; i < 2; i++){
if (ch[i] != null) ch[i]->addIt(add);
}
add = 0;
}
if (rev){
swap(ch[0], ch[1]);
for (int i = 0; i < 2; i++){
if (ch[i] != null) ch[i]->revIt();
}
rev = 0;
}
}
Node mem[maxn], *C = mem;
Node *make(int v){
C->sum = C->val = v;
C->rev = 0; C->add = 0;
C->mx = v;
C->ch[0] = C->ch[1] = null; C->isRoot = true;
C->p = null;
C->fa = null;
return C++;
}
void rot(Node *t){
Node *p = t->p;
p->relax();
t->relax();
bool d = t->d();
p->p->setc(t, p->d());
p->setc(t->ch[!d], d);
t->setc(p, !d);
p->upd();
if (p->isRoot){
p->isRoot = false;
t->isRoot = true;
t->fa = p->fa;
}
}
void pushTo(Node*t) {
static Node*stk[maxn]; int top = 0;
while (t != null) {
stk[top++] = t;
t = t->p;
}
for (int i = top - 1; i >= 0; --i) stk[i]->relax();
}
void splay(Node*u, Node*f = null) {
pushTo(u);
while (u->p != f) {
if (u->p->p == f)
rot(u);
else
u->d() == u->p->d() ? (rot(u->p), rot(u)) : (rot(u), rot(u));
}
u->upd();
}
Node *v[maxn];
vector<int> E[maxn];
int n, nQ;
int que[maxn], fa[maxn], qh = 0, qt = 0;
int wht[maxn];
void bfs()
{
qh = qt = 0;
que[qt++] = 1;
fa[1] = -1;
while (qh < qt){
int u = que[qh++];
for (int i = 0; i < E[u].size(); i++){
int e = E[u][i];
if (e != fa[u]){
fa[e] = u;
v[e]->fa = v[u];
que[qt++] = e;
}
}
}
}
Node *expose(Node *u)
{
Node *v;
for (v = null; u != null; v = u, u = u->fa){
splay(u);
u->ch[1]->setRoot(u);
u->setc(v, 1);
v->fa = u;
}
return v;
}
void makeRoot(Node *u)
{
expose(u);
splay(u);
u->revIt();
}
void addEdge(Node *u, Node *v)
{
makeRoot(v);
v->fa = u;
}
void delEdge(Node *u, Node *v)
{
makeRoot(u);
expose(v); splay(u); u->setc(null, 1); u->upd();
v->setRoot(null);
}
void addPath(Node *u, Node *v,int ax)
{
makeRoot(u);
expose(v);
splay(v);
v->addIt(ax);
}
ll sumPath(Node *u, Node *v)
{
makeRoot(u);
expose(v);
splay(v);
return v->sum;
}
ll maxPath(Node *u, Node *v)
{
makeRoot(u);
expose(v);
splay(v);
return v->mx;
}
Node *find_root(Node *u)
{
expose(u); splay(u);
while (u->ch[0] != null){
u = u->ch[0];
}
splay(u); return u;
}
int main()
{
while (cin >> n)
{
for (int i = 0; i <= n; i++) E[i].clear();
int ui, vi;
for (int i = 0; i < n - 1; i++){
scanf("%d%d", &ui, &vi);
E[ui].push_back(vi); E[vi].push_back(ui);
}
for (int i = 1; i <= n; i++){
scanf("%d", wht + i);
v[i] = make(wht[i]);
}
bfs();
cin >> nQ;
int oper, wi, xi, yi;
Node *nx, *ny;
while (nQ--){
scanf("%d", &oper);
if (oper == 3) scanf("%d%d%d", &wi, &xi, &yi);
else scanf("%d%d", &xi, &yi);
nx = v[xi]; ny = v[yi];
if (oper == 1){
if (find_root(nx) == find_root(ny)) puts("-1");
else{
addEdge(nx, ny);
}
}
else if (oper == 2){
if (find_root(nx) != find_root(ny) || xi == yi) puts("-1");
else{
makeRoot(nx);
expose(ny);
splay(ny);
Node *tmp = ny->ch[0];
ny->ch[0] = null; ny->upd();
tmp->setRoot(null);
}
}
else if (oper == 3){
if (find_root(nx) != find_root(ny)) puts("-1");
else{
addPath(nx, ny, wi);
}
}
else{
if (find_root(nx) != find_root(ny)) puts("-1");
else printf("%d\n", maxPath(nx, ny));
}
}
puts("");
}
return 0;
}
HDU4010 Query on The Trees(LCT),布布扣,bubuko.com
HDU4010 Query on The Trees(LCT)
原文地址:http://www.cnblogs.com/chanme/p/3836557.html