标签:style blog http 2014 for io
Dijkstra算法解决了有向图G=(V,E)上带权的单源最短路径问题,但要求所有边的权值非负。
Dijkstra算法是贪婪算法的一个很好的例子。设置一顶点集合S,从源点s到集合中的顶点的最终最短路径的权值均已确定。算法反复选择具有最短路径估计的顶点u,并将u加入到S中,对u
的所有出边进行松弛。如果可以经过u来改进到顶点v的最短路径的话,就对顶点v的估计值进行更新。
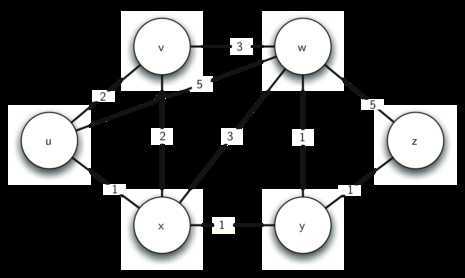
如上图,u为源点,顶点全加入到优先队列中。
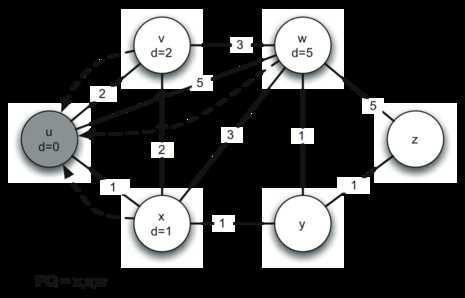
,队列中最小值为u(值为0),u出队列,对u的出边进行松弛(x、v、w),队列最小值为x。
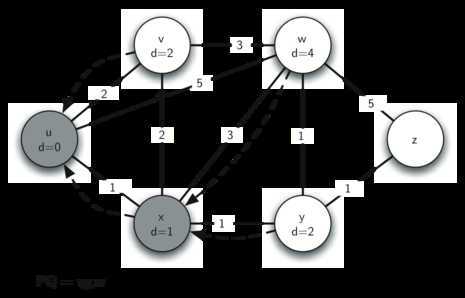
将x出列加入S,将x的出边松弛(v、y、w),其中w的值需要更新(4<5),队列最小值为v。
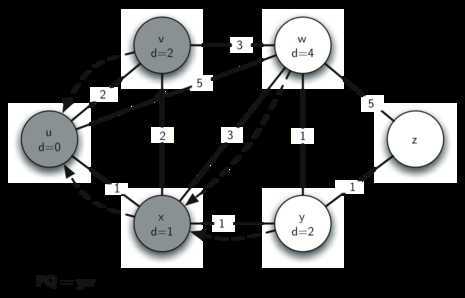
将v出列,加入到S中,将v的出边松弛(w),因x已在S中,故不做松弛。队列中的最小值为y。
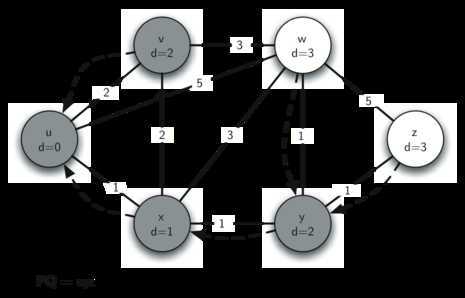
将y出列,y加入到S,松弛y的出边(w、z),更新w的值(3<4),队列最小值为w。
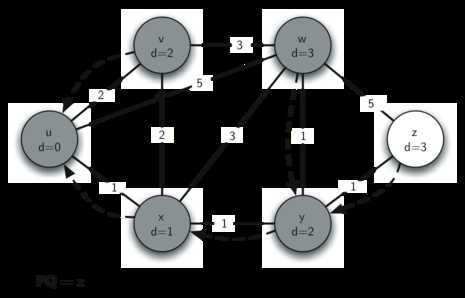
将w出列,加入到S中,松弛w的出边(z),队列最小值为z。
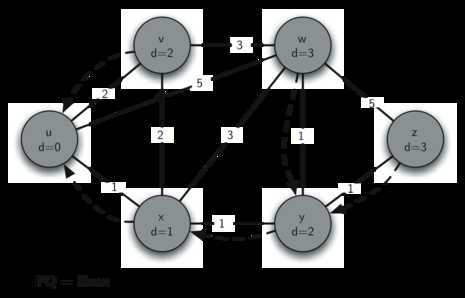
将z出列,加入到S中。将z的出边松弛(无),此时队列为空,算法结束。
Dijkstra算法的运行时间依赖于最小优先队列的具体实现。如果简单的运用数组实现求最小值,运行时间为O(V2+E)=O(V2)。
如果图比较稀疏,E=o(V2/lgV),如果用二叉最小堆实现,则为O((V+E)lgV)。
如果用斐波那契堆实现,可以提升到O(VlgV+E)。
import sys
class Vertex(object):
def __init__(self,key):
self.id=key
self.adj={}
def addNeighbor(self,nbr,weight=0):
self.adj[nbr]=weight
def getNeighbors(self):
return self.adj.keys()
def getId(self):
return self.id
def getWeight(self,key):
return self.adj[key]
class Graph(object):
def __init__(self):
self.vertexlist={}
self.size=0
def addVertex(self,key):
vertex=Vertex(key)
self.vertexlist[key]=vertex
self.size+=1
return vertex
def getVertex(self,key):
return self.vertexlist.get(key)
def __contains__(self,key):
if key in self.vertexlist:
return True
else:
return False
def addEdge(self,f,t,weight=0):
if f not in self.vertexlist:
self.addVertex(f)
if t not in self.vertexlist:
self.addVertex(t)
self.vertexlist[f].addNeighbor(self.vertexlist[t],weight)
def getVertices(self):
return self.vertexlist.keys()
def __iter__(self):
return iter(self.vertexlist.values())
def Dijkstra(G,s):
path={}
vertexlist=[]
for v in G:
vertexlist.append(v)
path[v]=sys.maxsize
path[s]=0
queue=PriorityQueue(path)
queue.buildHeap(vertexlist)
while queue.size>0:
vertex=queue.delMin()
for v in vertex.getNeighbors():
newpath=path[vertex]+vertex.getWeight(v)
if newpath<path[v]:
path[v]=newpath
queue.perUp(v)
return path
class PriorityQueue(object):
def __init__(self,path):
self.path=path
self.queue=[]
self.size=0
def buildHeap(self,alist):
self.queue=alist
self.size=len(alist)
for i in xrange(self.size/2-1,0,-1):
self._perDown(i)
def delMin(self):
self.queue[0],self.queue[-1]=self.queue[-1],self.queue[0]
minvertex=self.queue.pop()
self.size-=1
self._perDown(0)
return minvertex
def perUp(self,v):
i=self.queue.index(v)
self._perUp(i)
def _perUp(self,i):
if i>0:
if self.path[self.queue[i]]<=self.path[self.queue[(i-1)/2]]:
self.queue[i],self.queue[(i-1)/2]=self.queue[(i-1)/2],self.queue[i]
self._perUp((i-1)/2)
def _perDown(self,i):
left=2*i+1
right=2*i+2
little=i
if left<=self.size-1 and self.path[self.queue[left]]<=self.path[self.queue[i]]:
little=left
if right<=self.size-1 and self.path[self.queue[right]]<=self.path[self.queue[little]]:
little=right
if little!=i:
self.queue[i],self.queue[little]=self.queue[little],self.queue[i]
self._perDown(little)
if __name__==‘__main__‘:
g= Graph()
g.addEdge(‘u‘,‘x‘,1)
g.addEdge(‘u‘,‘v‘,2)
g.addEdge(‘u‘,‘w‘,5)
g.addEdge(‘x‘,‘v‘,2)
g.addEdge(‘x‘,‘y‘,1)
g.addEdge(‘x‘,‘w‘,3)
g.addEdge(‘v‘,‘w‘,3)
g.addEdge(‘y‘,‘w‘,1)
g.addEdge(‘y‘,‘z‘,1)
g.addEdge(‘w‘,‘z‘,5)
u=g.getVertex(‘u‘)
path=Dijkstra(g,u)
for v in path:
print v.id,path[v]
图论(四)------非负权有向图的单源最短路径问题,Dijkstra算法,布布扣,bubuko.com
图论(四)------非负权有向图的单源最短路径问题,Dijkstra算法
标签:style blog http 2014 for io
原文地址:http://www.cnblogs.com/linxiyue/p/3833971.html