标签:
说到逆运动学(IK),其中最重要的一部分就是利用雅克比矩阵表示目标状态和变量组之间的关系。具体文献参考“Introduction to Inverse Kinematics with Jacobian Transpose, Pseudoinverse and Damped Least Squares methods”。我们今天主要介绍雅克比矩阵在正运动学中的推导和应用。可能会用到一些我以前写的一篇关于坐标变换的相关知识,有兴趣的可以翻阅一下。
现在先假设我们已经知道一些先验知识,比如机械臂是由一些关节(Joint)连接的,一直从基座(base)连接到末端控制器(End-Effector),关节一般只有一个自由度(要么是旋转,要么是平移),末端控制器有六个自由度。如图1所示,我们已经将机械臂的结构描述的很清楚了。我们现在就是要解决,如何通过每一个关节的自由度求出末端控制器的六个自由度。这里在引入一个瞬时动力学的概念,就是任意关节运动,末端控制器也会跟着运动,如果时间足够小的话,我们可以看作关节和末端控制器都是瞬时变化的。现在我们问题也就转变成找ΔQ(关节的变化)和ΔX(末端控制器的变化)之间的关系。
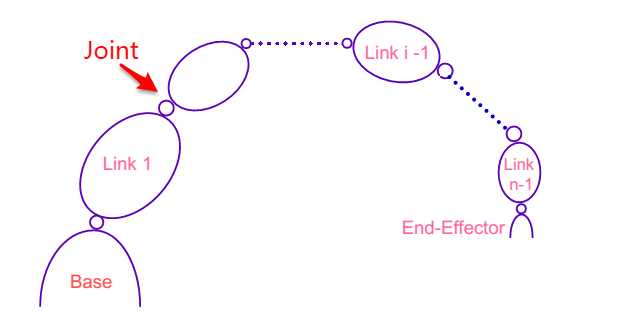
图1
我们先确定一些变量,我们对于旋转关节(revolute)一般讨论的是角度的变化,对于平移关节(prismatic)一般讨论的是距离的变化。这里为了统一表示,我们将角度和距离统称为通道量,记为q。同时,我们将目标状态(就是指末端控制器的六个自由度)记为向量组X={x1,x2,x3,x4,x5,x6}。好了,准备工作差不多了,现在我们来推导公式了。我们假设X中的每一项都是由q求出来的(事实上也是如此),记为x=f(q)。这样我们可以得到一组等式:
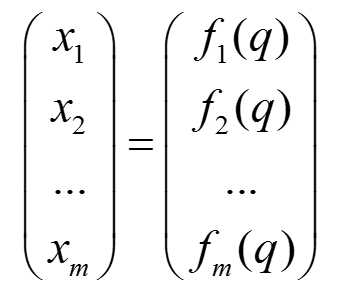
图2
根据上面等式,我们可以进行扩展。我们对X中的每一项进行全微分,等式的右边对所有的q进行偏导。具体展开式如下 , 另外我们可以将图3左边的展开式转化成右边的矩阵形式:
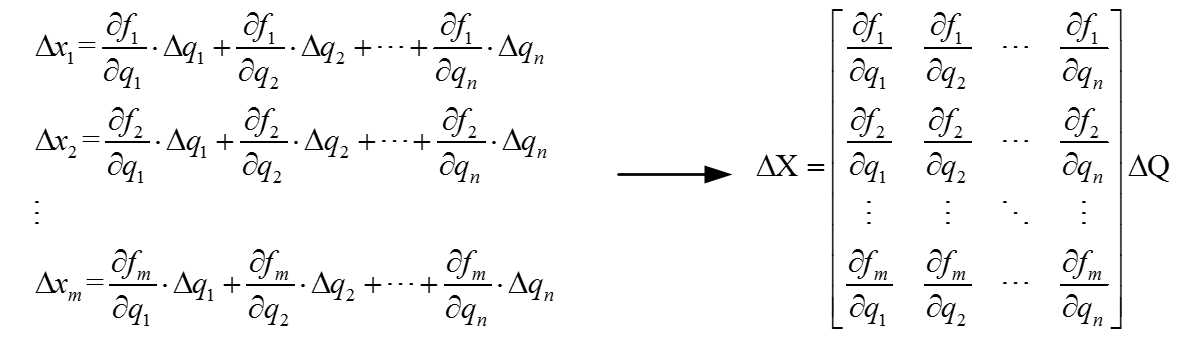
图3
可以发现一些结论,比如矩阵的行等于X中的项数m,也就是末端控制器的自由度个数,而矩阵的列等于Q中的项目数,也就是关节的个数。我们现在很自然的将上文中提到的ΔQ和ΔX联系起来了。这里得到的这个矩阵我们一般称为雅克比矩阵(Jacobian Matrix),记为J。上面的等式可以简写成:
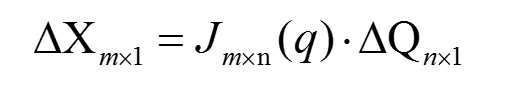
图4
这里,雅克比矩阵的推导就完成了。雅克比主要联系的是ΔQ和ΔX,是瞬时运动学的重要组成部分。在机器人学中,雅克比矩阵主要是用来求末端控制器的角速度和线速度,ΔQ和ΔX在时间片很小的情况下是可以用来表示速度的。在逆运动学中,我们通常利用末端控制器的自由度反算每个节点的自由度,这是我们只要将ΔX乘以雅克比矩阵的逆就可以得到Q的变化了。
今天先写到这,明天进行更进一步的分析。
标签:
原文地址:http://www.cnblogs.com/caster99/p/4725914.html