标签:
一、单链表结点的删除
0、删除单链表p指向的那个元素,(时间和空间复杂度尽量小)
二、单链表的存取
1、找出单链表的倒数第K个元素,(仅允许遍历一遍链表)
2、找出单链表的中间元素,(仅允许遍历一遍链表)
三、单链表与环的问题
3、判断单链表是否有环(6形状)?
4、如何找到环的入口?
5、如何知道环的长度?
6、带环链表的长度是多少?
四、单链表与相交、环的问题
7、如何知道两个单链表(无环)是否相交
8、如果两个单链表(无环)相交,如何知道它们相交的第一个节点是什么
9、如何知道两个单链表(有环)是否相交
10、如果两个单链表(有环)相交,如何知道它们相交的第一个节点是什么
~~~~~~~~~~~华丽的分割线~~~~~~~~~~~~~~

思路:把q指向结点的值 赋给 p指向的结点,再把q指向结点删除
思路:使用指针追赶的方法。使用两个指针fast和slow,只是fast每次走一步,slow每次走两步。当fast到头时,slow指向链表的中间元素
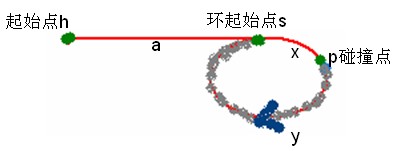
思路:使用指针追赶的方法,设定两个指针fast、slow,从头指针开始,每次分别前进1步、2步。如存在环,则两者相遇;如不存在环,fast遇到NULL退出。
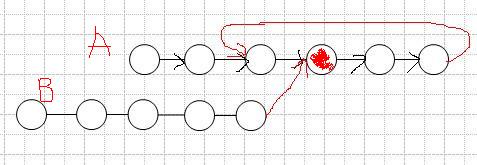
图说明:如上图,h是链表起始点,s是环入口,p是两个指针碰撞点。r = x + y
可以证明, a = y + mr (头指针 到 环入口的距离 = 碰撞点p 到 环入口的距离 + 循环多次环 )
附录处有证明
思路:令两个指针分别从第一个结点、碰撞点开始走,每一次走一步,直到两指针相遇,此时相遇的那个点就是环入口
思路:记录下问题4的碰撞点p(或者找在环中任意一结点都可以),让slow从碰撞点开始,绕着环走一圈,再次到碰撞点的位置时,所走过的结点数就是环的长度s。(一个指针从起始点出发走一圈,再次到起始点,就是走了环一圈)
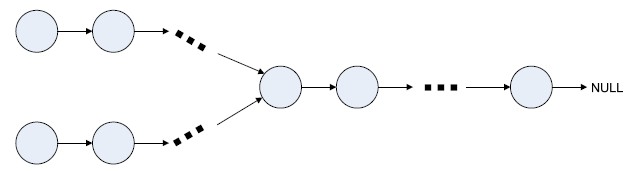
思路:
1、判断两链表最后一个节点是否相同,如果相交,则尾节点肯定是同一节点。
时间复杂度O((length(A)+ length(B))、空间复杂度 = O(1)(存储最后结点的地址)
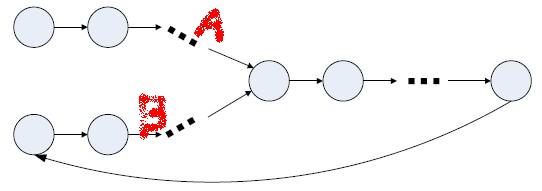
2、人为构环,如上图。将链表A的尾节点指向链表B,如果B链表有环,则两个链表相交,此时从链表B的头指针往下遍历,如果能够回到B,则说明相交
时间复杂度O((length(A)+ length(B)),没有额外的空间消耗
思路:
1、先取得两个链表A和B的长度len(A)和len(B)
2、沿着A和B链表中较长的链表遍历,使用指针追赶的方法。
设定两个指针fast、slow。fast先出发前进(lengthMax-lengthMin)步(即是二者的长度之差)使fast和slow指针到相交点的距离相等,之后两个链表同时前进,每次一步,相遇的第一点即为两个链表相交的第一个点。
思路:根据两个链表是否有环来分别处理
1、如果两个链表都没有环。可用 问题7 来判断
2、一个有环,一个没环。肯定不相交
3、两个都有环。(注,两个有环链表相交是指这个环属于两个链表共有)
具体方法:如果两个都有环,则求出A的环入口,判断其是否在B链表上,如果在,则相交。
或者,在A链表上,使用指针追赶的方法,找到两个指针碰撞点,之后判断碰撞点是否在B链表上。如果在,则相交 。
(注,两个有环链表相交是指这个环属于两个链表共有)
情况1:相交的点,在环外
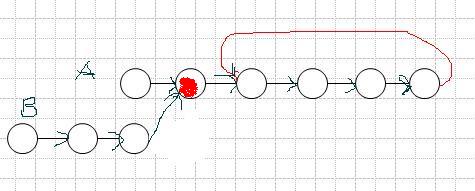
思路:使用指针追赶的方法。
1、求两个链表A和B的长度Length(A)和Length(B)
2、如果Length(A)> Length(B),则链表A指针先走 Length(A)- Length(B),链表B指针再开始走,则两个指针相遇的位置就是相交的第一个节点。
如果 Length(B)> Length(A),则链表B指针先走 Length(B)- Length(A),链表A指针再开始走,则两个指针相遇的位置就是相交的第一个节点。
情况2(图2)、相交的点,在环内,还不能处理
分析:当交点在环中时,此时的交点可以是A链表中的环入口点,也可以是B链表中环入口点。
为什么这么说?这是因为如果把B看出一个完整的链表,而A指向了B链表,则此时交点是A的环入口点。反之交点是链表B的环入口点。
思路:根据上述分析,可以直接求出A的环入口点或者B的环入口点就可以了。
综合这两种情况,给出两个方法求出结点
方法一、先检测交点是否在第一种情况中。如果是,则直接输出该结点。如果不是,则直接输出任意一个环交点。
方法二、使用哈希,只需要把链表A或者B所有的元素全部放入哈希表中,之后把B链表或者A链表中的每一个元素去哈希探测,即可找到交点。
4、如何找到环的入口?
图说明:如图,h是链表起始点,s是环入口,p是两个指针碰撞点。r表示环的长度,r = x+y
可以证明, a = y + mr (头指针 到 环入口的距离 = 碰撞点p 到 环入口的距离 + 循环多次环 )

证明:
当fast若与slow相遇时,slow肯定没有走遍历完链表,而fast已经在环内循环了n圈(1<=n)。
假设slow走了s步,则fast走了2s步(fast步数还等于s 加上在环上多转的n圈)。
设环长为r,则:
2s = s + nr,即s= nr设整个链表长L,入口环与相遇点距离为x,起点到环入口点的距离为a。
s = nr
a + x = nr
a + x = (n – 1)r +r = (n-1)r + r
a = (n-1)r + r - x
a = (n-1)r + y
由此可知,从链表头到环入口点等于(n-1)循环内环+ 相遇点到环入口点,于是我们从链表头、与相遇点分别设一个指针,每次各走一步,两个指针必定相遇,且相遇第一点为环入口点。
版权声明:本文为博主原创文章,未经博主允许不得转载。
标签:
原文地址:http://blog.csdn.net/frimish/article/details/47668325