标签:
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 12817 | Accepted: 3343 |
Description
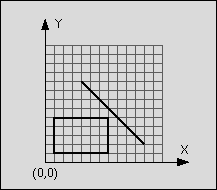
Input
Output
Sample Input
1 4 9 11 2 1 5 7 1
Sample Output
F
Source
#include <iostream> #include <stdio.h> #include <algorithm> #include <string.h> #include <cmath> #define eps 1e-8 #define maxn 100 using namespace std; int sgn(double x) { if(abs(x) < eps) return 0; if(x<0) return -1; else return 1; } struct Point { double x; double y; Point(){} Point(double _x,double _y) { x = _x; y = _y; } Point operator -(const Point &a) const { return Point(x-a.x,y-a.y); } Point operator + (const Point &a) const { return Point(x+a.x,y+a.y); } double operator *(const Point &a) const { return x*a.x+y*a.y; } double operator ^(const Point &a) const { return x*a.y-y*a.x; } }; struct Line { Point s; Point e; Line(){} Line(Point _s,Point _e) { s = _s; e = _e; } }; ///判断线段相交 bool inter(Line l1,Line l2) { return max(l1.s.x,l1.e.x) >= min(l2.s.x,l2.e.x) && max(l2.s.x,l2.e.x) >= min(l1.s.x,l1.e.x) && max(l1.s.y,l1.e.y) >= min(l2.s.y,l2.e.y) && max(l2.s.y,l2.e.y) >= min(l1.s.y,l1.e.y) && sgn((l2.s-l1.e)^(l1.s-l1.e))*sgn((l2.e-l1.e)^(l1.s-l1.e)) <= 0&& sgn((l1.s-l2.e)^(l2.s-l2.e))*sgn((l1.e-l2.e)^(l2.s-l2.e)) <=0; } ///判断直线和线段是否相交 bool seg_inter_line(Line l1,Line l2) { return sgn((l2.s-l1.e)^(l1.s-l1.e))*sgn((l2.e-l1.e)^(l1.s,l1.e)) <=0; } bool Onseg(Point p,Line L) { return sgn((L.s-p)^(L.e-p)) == 0 && sgn((p.x-L.s.x)*(p.x-L.e.x)) <= 0 && sgn((p.y-L.s.y)*(p.y-L.e.y)) <= 0; } int inConvexpoly(Point a,Point p[],int n) { for(int i=0;i<n;i++) { if(sgn((p[i]-a)^(p[(i+1)%n]-a)) < 0) return -1; else if(Onseg(a,Line(p[i],p[(i+1)%n]))) return 0; } return 1; } int main() { //freopen("in.txt","r",stdin); int T; scanf("%d",&T); while(T--) { Point s; Point e; double x1,y1,x2,y2; scanf("%lf %lf %lf %lf %lf %lf %lf %lf",&s.x,&s.y,&e.x,&e.y,&x1,&y1,&x2,&y2); if(x1 > x2) swap(x1,x2); if(y1 > y2) swap(y1,y2); Point p[10]; Line L = Line(s,e); p[0] = Point(x1,y1); p[1] = Point(x2,y1); p[2] = Point(x2,y2); p[3] = Point(x1,y2); if(inter(L,Line(p[0],p[1]))) { printf("T\n"); continue; } else if(inter(L,Line(p[1],p[2]))) { printf("T\n"); continue; } else if(inter(L,Line(p[2],p[3]))) { printf("T\n"); continue; } else if(inter(L,Line(p[3],p[0]))) { printf("T\n"); continue; } else if(inConvexpoly(L.s,p,4)>=0 || inConvexpoly(L.e,p,4)>=0) { printf("T\n"); continue; } else printf("F\n"); } return 0; }
标签:
原文地址:http://www.cnblogs.com/chenyang920/p/4733155.html