标签:
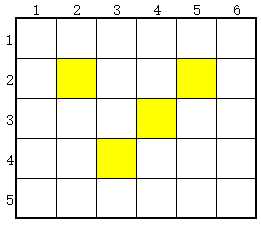
题意:如上图的一块板子,其中部分格子已经亮起,每当按下一个格子,其上下左右及自己共5个格子的亮暗状态会改变(亮变暗,暗变亮)。给定一块板子的初始状态,问要使得每个格子都亮起来,需要按多少次,以及按哪些格子?
思路:
(1)对于任意一个格子,如果这个格子改变了偶数次状态,则等价于没有发生改变。我们可以将1看作格子亮着,0看作格子暗着,每改变1次就加1,最后格子的状态等于其总数值 MOD 2。则其运算结果刚好满足异或运算,即每改变一次等于状态值 xor 1。
(2)对于一个格子x和它周围的4个格子来说,若格子x被按下偶数次,它自身和周围4个格子的状态也等于没有发生改变。所以我们可以知道:任意一个格子至多被按下一次。
(3)假设有数组x[1..30],分别表示这30个格子是否按下1次,若按下则x[i]=1,否则x[i]=0。则对于1个格子,他最后的状态为:
当前状态 = 初始状态 xor (a[1] * x[1]) xor (a[2] * x[2]) xor ... xor (a[30] * x[30]);
a[i]表示第i个格子是否受这个格子的影响,按一次最多只能影响5个,若在边界上可能还更少。
因为我们的目标是要让所有等格子都为亮的状态,故我们需要让 当前状态 = 1,再将式子变换一下:
(a[1] * x[1]) xor (a[2] * x[2]) xor ... xor (a[30] * x[30]) = 1 xor 初始状态;
那么右边的就完全知道了,而左边只是知道a数组,要求的就是x数组了。上面仅仅是由一个格子所列出的式子,所以一共得列出30条式子才行,再进行高斯消元。大概是如下的:
(a[ 1][1] * x[1]) xor (a[ 1][2] * x[2]) xor ... xor (a[ 1][30] * x[30]) = y[1];
(a[ 2][1] * x[1]) xor (a[ 2][2] * x[2]) xor ... xor (a[ 2][30] * x[30]) = y[2];
.......此处省略27条式子.....................
(a[30][1] * x[1]) xor (a[30][2] * x[2]) xor ... xor (a[30][30] * x[30]) = y[30];
(4)消元方法:方法和普通消元方法差不多,唯一变的是,若要消去a[j][i],不再用加减法,而是用xor。将第i行与第j行分别左边与左边,右边与右边相异或,作为第j行的结果。
(a[j][1] * x[1]) xor (a[j][2] * x[2]) xor ... xor (a[j][30] * x[30]) xor (a[i][1] * x[1]) xor (a[i][2] * x[2]) xor ... xor (a[ i][30] * x[30]) = y[j] xor y[i]
=> ((a[j][1] * x[1]) xor (a[i][1] * x[1])) xor (((a[j][2] * x[2]) xor (a[i][2] * x[2]))) xor ... xor ((a[j][30] * x[30]) xor (a[i][30] * x[30])) = y[j] xor y[i]
=> ((a[j][1] xor a[i][1]) * x[1]) xor ((a[j][2] xor a[i][2]) * x[2]) xor ... ((a[j][30] xor a[i][30]) * x[30]) = y[j] xor y[i]
总的来说,就是((a[j][1] * x[1]) xor (a[i][1] * x[1]))可以变成 ((a[j][1] xor a[i][1]) * x[1]) 。注意,如果a[j][i]本来就为0,这一步完全可省。消完之后从后面开始逐步进行代入就可以求出所有的x[i]了。

1 #include <bits/stdc++.h> 2 #define max(X,Y) ((X) > (Y) ? (X) : (Y)) 3 #define min(X,Y) ((X) < (Y) ? (X) : (Y)) 4 #define pii pair<int,int> 5 #define INF 0x7f7f7f7f 6 #define LL long long 7 using namespace std; 8 const int N=30; 9 const int M=50; 10 int x[M]; 11 int r[M]; 12 int y[M]; 13 int a[M][M]; 14 15 16 void GE() 17 { 18 memset(a, 0, sizeof(a)); 19 memset(y, 0, sizeof(y)); 20 memset(x, 0, sizeof(x)); 21 22 for(int i=1; i<=N; i++) //初始化 23 y[i]=1^r[i]; //等式右边 24 25 for(int i=1; i<=N; i++) //第i个格子的四周4个 26 { 27 a[i][i]=a[i][i+6]=1; 28 if(i-6>0) a[i][i-6]=1; 29 if(i%6!=0) a[i][i+1]=1; 30 if(i%6!=1) a[i][i-1]=1; 31 } 32 33 for(int i=1; i<=N; i++) 34 { 35 for(int j=N; j>=i; j--) //找到某行第i列非0的,换到第i行。 36 { 37 if(a[j][i]) 38 { 39 swap(a[i], a[j]); 40 swap(y[i], y[j]); 41 break; 42 } 43 } 44 45 //消去其他行的第i列 46 for(int j=i+1; j<=N; j++) 47 { 48 if(a[j][i]) //为1的才要消 49 { 50 a[j][i]=0; 51 for(int k=i+1; k<=N; k++) a[j][k]^=a[i][k]; 52 y[j]^=y[i]; 53 } 54 } 55 } 56 57 //回代 58 for(int i=N; i>=1; i--) //对于第i行,只需要算出第i列的x。 59 { 60 for(int j=N; j>i; j--) y[i]^=x[j]*a[i][j]; //反向回代 61 x[i]=y[i]; //a[i][i]已经保证为1了。 62 } 63 64 } 65 66 int main() 67 { 68 freopen("input.txt", "r", stdin); 69 char c; 70 for(int i=1; i<=N; i++) 71 { 72 c=getchar(); 73 if(c==‘0‘ || c==‘1‘) r[i]=c-‘0‘; 74 else i--; 75 } 76 77 GE(); 78 79 int cnt=0; 80 for(int i=1; i<=N; i++) if(x[i]) cnt++; 81 printf("%d\n", cnt); 82 for(int i=1; i<=N; i++) if(x[i]) printf("%d %d\n", (i-1)/6+1, (i-1)%6+1); 83 84 return 0; 85 }
标签:
原文地址:http://www.cnblogs.com/xcw0754/p/4733761.html