标签:
动态规划,给定长度为n(≤1e6)的整数数组和整数m,选取m个连续且两两无交集的子区间,求所有方案中使得区间和最大的最大值。
dp[i][j]表示结束位置(最后一个区间最后一个元素的位置)为i且选取区间数为j的最大值。
容易得到以下状态转移方程:
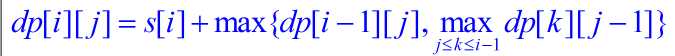
又:
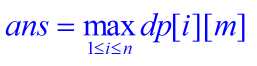
考虑到数组的规模和j的更新特征,使用一维滚动数组取代二维数组,最外层循环枚举j到m即可。
用dp[0][i]表示dp[i][j], dp[1][i]表示max(dp[k][j-1]) (k≤i)。
复杂度为O(n^2) 。

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 5 using namespace std; 6 typedef __int64 LL; 7 8 const int inf = 0x3f3f3f3f; 9 const int maxn = 1e6 + 10; 10 11 int s[maxn]; 12 LL dp[2][maxn]; 13 LL ans, maxi; 14 int n, m; 15 16 int main(){ 17 while(~scanf("%d%d", &m, &n)){ 18 for(int i = 1; i <= n; i++) scanf("%d", &s[i]); 19 ans = maxi = -inf; 20 memset(dp, 0, sizeof dp); 21 int o = 1; 22 for(int j = 1; j <= m; j++){ 23 maxi = -inf; 24 for(int i = j; i <= n; i++){ 25 dp[0][i] = s[i] + max(dp[0][i - 1], dp[1][i - 1]); 26 } 27 for(int i = j; i <= n; i++) maxi = dp[1][i] = max(maxi, dp[0][i]); 28 } 29 for(int i = m; i <= n; i++) ans = max(ans, dp[0][i]); 30 printf("%I64d\n", ans); 31 } 32 return 0; 33 }

标签:
原文地址:http://www.cnblogs.com/astoninfer/p/4734736.html