标签：
【转载时请注明来源】：http://www.cnblogs.com/aria313
——根据Andrew Ng 2008年课程的第1~4节，以及相关的讲义notes 1，进行总结
网易公开课地址：http://study.163.com/plan/planMain.htm?id=1200146
2015.8.14
监督学习Supervised learning:
有样本集合，样本是标准的正确答案；以此为根据学习，得到函数h()，以后再有输入x，便可根据函数得到输出y；
其本质如下图：
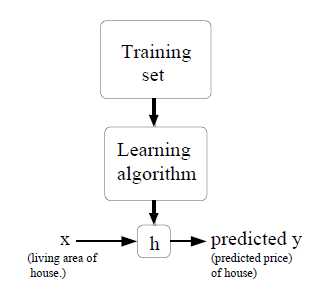
需解决的关键核心问题是：
核心问题1：h()函数的形式，应该是怎样的？
核心问题2：h()函数中的参数个数？
核心问题3：需要一个标准，确定这些参数是不是最优的？
核心问题4：需要一个算法，使我们，可以通过已有的样本集合，得到上述定义下的最优参数；
假设读者已经读完了Andrew的讲义notes 1，接下来会打乱notes 1中的顺序，提纲挈领的理顺其中的方法学逻辑。
Notation：
GLM：Generalized Linear Models 广义线性模型
regression：回归问题：输出值Target连续的问题
classification：分类问题：输出值不连续
linear regression： 线性回归问题
LMS： least mean squares algorithm 最小均方算法，用来解决线性回归问题的算法
gradient descent：梯度递减算法，一个找函数最小值的算法；
The normal equations：正定方程，用矩阵计算的方法，直接求出线性回归中的最优参数；不用迭代逼近；
LWR：Locally weighted linear regression局部加权线性回归；当对某个输入点做输出估计时，只求出该点附近的线性函数，有点像切线的样子；
首先讨论“核心问题3：需要一个标准，确定这些参数是不是最优的？”；我们先认为核心问题1和2已经解决；
答案：似然函数的值取到最大时，参数向量θ最优；
解释：
在现实世界中，影响因素是极其多样的，无论输入特征值x有多少维，都不可能完整的描述某个事物的全部。比如，在一个购房事件中，即使房屋的特征已经描述，影响购房事件的还有买卖双方的心情等等。因此，在现实世界中，因为有其他的不可控因素，即使输入特征值x不变，输出值y是变化的。
所以：y是给定x条件下的随机变量；
一个样本 (x(1),y(1)) 其实是该随机变量的一次采样；我们在确定h() 形式的同时，其实也确定了一种概率分布类型；因此，在给定参数θ和输入x(1)后，输出y的概率分布就已经确定了：P(y|x= x(1); θ)
但其实y= y(1)已经发生，其发生概率P(1)= P(y= y(1)|x= x(1); θ)，那么什么样的参数θ最合理呢？最自然的想法是，在该参数θ下，P(1)越大越自然；
在给定样本 (x(1),y(1))后，上述概率其实是θ的函数L(θ)，称为似然函数；
当样本集合不只有一个样本，而是m个样本，一般我们都会假设每个样本间是互相独立的。于是，考虑整个样本集合，似然函数变为
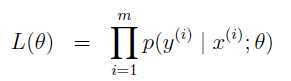
似然函数L(θ)，输入是θ，输出是样本集合发生的概率；
答案：h()是一个概率分布的期望值的表达式，该概率分布由θ、x决定；
（在讲义notes 1中，Andrew把该概率分布函数 限制在 指数函数族 的范围内）
解释：
如上节所述，在输入x确定后，由于其他因素的不可控，其输出y其实为一个随机变量。而h()要给出y的最好估计值，自然地我们会用到期望值E(y|x; θ)；
其中，θ由样本集合训练而得；x是训练完成后，你使用模型时的输入。
至于该概率分布是哪一种分布，则需根据具体事务的特点去假设；
比如说：分布是高斯分布，则h(x)= E(y|x; θ)=μ，μ在给定x、θ后是确定的；
答案：用GLM构造方法
解释：
假设了一个概率分布种类后，其概率分布函数的形式就已经知道了，比如伯努利分布（参数φ，代表某事物为真的概率）：
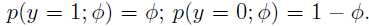
比如泊松分布（参数λ，代表单位时间内访问顾客数量期望）：
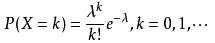
这些概率分布函数虽然知道，但我们需要的是P(y|x; θ)：即在给定θ、x的情形下，确定该分布函数中的参数，比如上面的φ、λ；
用到的方法是GLM构造法，该构造法基于 指数函数族 和 3个假设
（1）指数函数族The exponential family
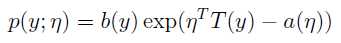
当a(), b(), T() 确定后，该函数族可代表一个分布随η变化的概率分布函数；
选取不同的a、b、T，函数族可以变形为各种常见的分布类型，如：高斯分布、伯努利分布、多项式分布、泊松分布、指数分布、γ分布、β分布、Dirichlet分布，等等；
（2）3个假设
i) 给定x、θ，P(y|x; θ)函数属于指数函数族
ii) h(x)= E(y|x; θ)
iii) η = θT x
前两个假设，其实前文已经表述原因了，关键是第3个假设，可以看出它是线性的。我猜想，这也是为什么该模型称为“广义线性模模型”的原因；
GLM构造的具体步骤如下：
（1）假设我们学习的事物符合某种分布，则该种分布的概率分布函数（带一个自有参数）就已知了；
（2）把已知的概率分布函数 做数学变化，转化为 指数函数族的形式，于是得出a(), b(), T()，以及最重要的：把η用自有参数来表示（自有参数是比如：伯努利分布中的φ，泊松分布中的λ）
（3）又由于η = θT x，所以可由x、θ求得某种分布自有参数的值，其期望E(y|x; θ)自然就求出来了。
于是，h(x)= E(y|x; θ) 具体表达式确定。
举例说明：
判断肿瘤是良性还是恶心，输出y=0或1，输入x向量为描述肿瘤的各种信息；
（1）自然假设y属于伯努利分布，y只能取0或1；
（2）变化为 指数函数族 的形式：
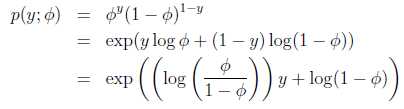
得：
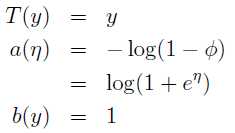
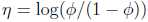
（3）反向带入，可得：
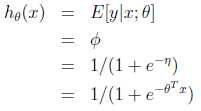
这就是logistic回归问题，是二元分类问题。
同理，若假设y属于高斯分布，则会自然推导出线性回归问题。
所以，线性回归、logistic回归统一在该方法论下。
接下来讨论“核心问题4：需要一个算法，使我们，可以通过已有的样本集合，得到上述定义下的最优参数”
答案：本质就是找似然函数L(θ)的最大值对应的θ是多少；
Notes 1介绍了三个算法：梯度递增/减算法，牛顿算法；正定方程法；
详解：（注意：对L(θ)求最大值时，通常先对其取对数，以方便计算）
梯度递增/减算法：不再累述；就是一步一步走，有两种常用的迭代策略，一是batch批量，遍历所有样本集合，再更新θ，二是stochastic随机，每次处理一个样本，就更新θ，适合样本集合太大的情况；
牛顿算法：牛顿算法是用来求过零点的；所以在运用上，是把log(L(θ))的导数求出来，然后用牛顿法，求其导数的零点。
正定方程法：该方法其实只适用于线性回归；具体是指，若h(x)应用于样本集合里的所以x(i)，都可以求得相应的y(i)，一丝不差；则，下面的等式会成立：
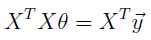
这就是正定方程。于是，θ可由下列方程直接算出来：
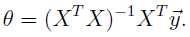，若矩阵的逆不存在，则用最小二乘找近似的；
PS：跑偏一下，由“矩阵是否可逆”引发的关于“矩阵物理意义”的思考：
我们知道，如果矩阵的行列式不等于0，矩阵就是可逆的。为什么呢？
（1）矩阵是在一个空间内，对“物体”进行 转换变化操作；
比如，在二维空间内(1,2)并不是代表一个点，而是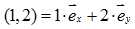
，代表一个矩形面。数字1和2只是代表某个基的倍数而已，(1,2)去乘某个矩阵如下，只是换基而已。
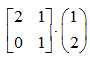
即(1,2)中的1，原来基是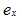
，变换后为
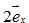；(1,2)中的2，原来基是
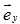，变换后为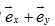
。数字1和2依然是代表谁谁谁的倍数，现在只是“谁谁谁”变了而已。
（2）行列式就是矩阵对应的线性变换对空间的拉伸程度的度量，或者说物体经过变换前后的体积比。
比如上面的矩阵行列式等于2，它就把一个矩形面(1,2)的“体积”(在二维定义下即面积)，拉伸了2倍，“体积”由2变为4。
（3）那行列式等于0，意味着矩阵对“物体”进行转化操作时，把“物体”降维了（想起了二向箔）。
行列式等于0，即矩阵不满秩，意味着换上去的新基，其实维度上少了一维。
比如下面矩阵变化，被操作的“物体”是一个矩形面(1,2)，经过变换后，它被变成了一个线。
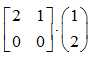
那么自然，它的“体积”(在二维定义下即面积)，由2变为了0。一旦降维，在度量上自然变为0。
（4）逆矩阵其实是一个逆向操作，把矩阵的变换操作给恢复回去。
那降维后，在信息上就有了缺失，这种缺失是无法挽回的了。所以这个逆向操作不存在，即逆矩阵不存在，矩阵不可逆。
讲义notes 1中关于参数个数讲的不多，只有少量关于欠拟合underfitting或过拟合overfitting的描述；
然后介绍了LWR：Locally weighted linear regression局部加权线性回归；当对某个输入点做输出估计时，只求出该点附近的线性函数，有点像切线的样子；
其中，权数函数，形似高斯分布，但没有任何概率论上的意义；只是表示，越靠近待估计点，权重越大；
然后，随着样本集合的样本数量变多，局部加权线性回归LWR，需要的参数向量的长度会相应变大；
Andrew机器学习课程的学习总结1：监督学习的一种方法论，广义线性模型（GLM）的方法学
标签：
原文地址：http://www.cnblogs.com/aria313/p/4735081.html
