标签:
素数专题
素数是一个经常的涉及到得内容,所以有必要整理出有关解决素数相关问题的算法
学习资料:Eratosthenes筛法和欧拉筛法对比 一般筛法求素数+快速线性筛法求素数 数学技巧之素数筛选
1 /*
2 约数枚举,复杂度O (sqrt(n))
3 By TiaoZhan
4 */
5 vector<int> divisor(int n)
6 {
7 vector<int> res;
8 for (int i=1; i*i<=n; ++i)
9 {
10 if (n % i == 0)
11 {
12 res.push_back (i);
13 if (n / i != i) res.push_back (n / i);
14 }
15 }
16
17 return res;
18 }
1 /*
2 整数分解,复杂度O(sqrt(n))
3 By TiaoZhan
4 */
5 map<int, int> prime_factor(int n)
6 {
7 map<int, int> res;
8 for (int i=2; i*i<=n; ++i)
9 {
10 while (n % i == 0) {++res[i]; n /= i;}
11 }
12 if (n != 1) res[n] = 1;
13
14 return res;
15 }
1 /*
2 素性测试,输入正数,复杂度O (sqrt(n))
3 By TiaoZhan
4 */
5 bool is_prime(int n)
6 {
7 for (int i=2; i*i<=n; ++i)
8 {
9 if (n % i == 0) return false;
10 }
11 return n != 1; //1例外
12 }

1 /*
2 此算法在小范围(1e5)内判素数个数以及单个数判素数有奇效,不适用于大范围判素数
3 */
4 bool is_prime(int x) {
5 if (x == 2 || x == 3) return true;
6 if (x % 6 != 1 && x % 6 != 5) return false;
7 for (int i=5; i*i<=x; i+=6) {
8 if (x % i == 0 || x % (i + 2) == 0) return false;
9 }
10 return true;
11 }
1 /*
2 埃氏筛法:返回n以内素数的个数, 复杂度O (nloglogn)
3 By TiaoZhan
4 */
5 int seive(int n) { //Eratosthenes (埃氏筛法)
6 int p = 0;
7 memset (is_prime, true, sizeof (is_prime));
8 for (int i=2; i<=n; ++i) {
9 if (is_prime[i]) {
10 prime[++p] = i;
11 for (int j=2*i; j<=n; j+=i) is_prime[j] = false;
12 }
13 }
14 return p;
15 }

1 /* 2 欧拉筛法:返回n以内素数的个数, 复杂度O (n) 3 */ 4 int seive2(int n) { //Euler (欧拉筛法) 5 int p = 0; 6 memset (is_prime, true, sizeof (is_prime)); 7 for (int i=2; i<=n; ++i) { 8 if (is_prime[i]) prime[++p] = i; 9 for (int j=1; j<=p && i*prime[j]<=n; ++j) { 10 is_prime[i*prime[j]] = false; 11 if (i % prime[j] == 0) break; 12 } 13 } 14 return p; 15 }
附上比较两种筛法的测试结果
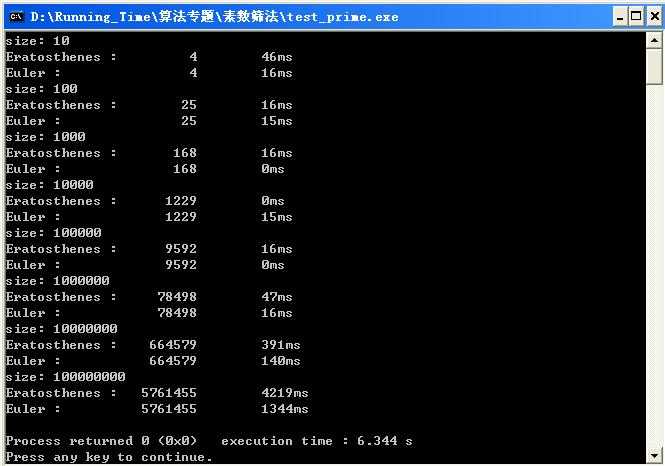
标签:
原文地址:http://www.cnblogs.com/Running-Time/p/4736142.html